Chapitre V Le matériel et les sources du nœud La première question que nous nous sommes posée, après avoir constaté, par l’analyse du nœud choisi comme exemple, que le nœud était un accomplissement de coupure, a été celle de savoir s’il s’agissait là d’un caractère général. Durant ce travail d’interprétation d’autres questions se sont présentées à notre esprit. Maintenant que le premier point est élucidé, nous pouvons aborder ces problèmes, quitte à perdre de vue un instant le motif de l’accomplissement de la coupure, dont l’étude n’est nullement achevée. Nous savons, grâce à notre travail d’interprétation, que nous pouvons découvrir dans les nœuds une partie nouage et une partie non-nouage. Nous devons nous hâter de réexaminer un par un les divers problèmes que pose le nœud et de chercher à résoudre par là des énigmes et des contradictions qui, aussi longtemps que l’on n’a connu que le nœud dans sa globalité, ont paru insolubles aux tentatives de classifications. Nous avons exposé, dans notre premier chapitre, les résultats mathématiques des auteurs qui se sont occupés du nœud sur les relations entre le nœud et l’espace qui lui donne lieu et ne se sont pas posés de question sur la provenance du matériel du nœud et sur la composition de ce matériel. Nous répondrons par là à la question de savoir à quoi tient la complication dans les nœuds et les chaînes. I. Description graphique Précisons ici trois particularités de la description des objets, jamais observées avant nous, pas encore expliquées : 1 — Les nœuds et les chaînes montrent deux parties, dites nouage et non-nouage, pouvant elles-mêmes être constituées de plusieurs composants. 2 — Les nœuds et les chaînes choisissent les composants de la partie nouage parmi les purs nœuds, de la partie non-nouage parmi les non-nœuds. 3 — Les nœuds et les chaînes disposent leurs parties selon un mode de composition bien particulier parmi les divers modes de composition constructibles, nous le dirons régulier et nous définirons ce type de montages réguliers. Ces particularités dans le choix des éléments des objets ont été bien entendu tirées d’observations faites sur les différentes parties du nœud. Nous étudierons dans ce chapitre la source de ces parties prises séparément. Nous étudierons la régularité du mode de composition de ses parties dans le chapitre suivant.
Fig. 1 Le premier nœud premier [2, Sém XX, p. 111], le nœud Trèfle, est un nœud proprement dit au sens mathématique du terme puisqu’il est fait du nouage d’un seul rond. Pour nous, dans notre façon de dire, il s’agit d’un nœud propre. a1 - La notion de nœud premier Définissons maintenant le mode de composition des nœuds qui conduit à la notion de nœud premier1. Nous pouvons raccorder deux nœuds en réunissant leurs surfaces d’empans respectives par un unique ruban.
Fig. 2 Du point de vue de la théorie des nœuds dans sa relation avec la théorie des surfaces, les nœuds faits avec de la ficelle sont homologues avec les nœuds du bord de la surface. Cette référence à la théorie des surfaces est une commodité, afin de bien définir les choses. De cette manière, d’un autre point de vue, les nœuds se trouvent disposés sur une ficelle qui forme un cercle. On peut composer de cette manière un nombre indéterminé de nœuds.
Si on ferme le cercle en réunissant les deux extrémités de cette figure, nous sommes bien en présence de nœuds qui sont disposés en cercles répartis le long d’une même corde.
La forme générale de cette composition consiste à réunir les nœuds par un carrefour de mise en continuité. Ce carrefour peut être conçu, toujours pour des raisons de commodité, comme un carrefour de rubans raccordant leur surface d’empan respective.
Pourvu de ce mode de composition, nous pouvons parler de la décomposition d’un objet en nœuds élémentaires. Ce sont les nœuds premiers. a2 - Le monoïde des nœuds premiers Ce mode de composition peut faire illusion, il peut faire croire à une certaine pertinence, du fait de présenter une structure qui a un nom en algèbre, c’est la structure de monoïde commutatif unitaire, mais cette structure algébrique est assez rudimentaire. Elle est associative au sens où la composition de deux nœuds, elle-même composée avec un troisième, équivaut à la composition du premier avec le composé des deux autres. Ceci s’écrit facilement, de telle manière que l’associativité se voit dans le jeu des parenthèses : (N1 # N2) # N3 = N1 # (N2 # N3) alors qu’elle ne se lit pas dans la présentation des trois nœuds sur une corde. Il est plus remarquable de constater que ce mode de composition est commutatif. On peut effectivement déplacer les nœuds dans leur ordre le long de la corde qui les réunit en cercle. Le lecteur peut en faire l’expérience en construisant un composé de nœuds et en cherchant à changer leur ordre circulaire. Il faut les faire passer les uns dans les autres, ce qui est toujours possible. Ce monoïde commutatif a un élément neutre puisque le rond simple dit aussi nœud trivial peut être composé avec d’autres nœuds. Le résultat de la composition ne change pas le composé de départ.
Par contre, il n’y a pas d’élément inverse, ce pourquoi nous parlons de structure de monoïde et nous ne parlons pas de groupe. Les nœuds premiers sont ceux qui restent indécomposables en éléments plus simples selon ce mode de concaténation. Ce point de vue établit une analogie avec les nombres premiers indécomposables par la multiplication, parmi les nombres entiers positifs qui présentent eux-mêmes une structure de monoïde lorsqu’ils sont composés aussi bien par l’addition que par la multiplication. Ce mode de composition ne tient pas compte de nos coloriages. Il est contemporain du premier temps de notre algorithme et il est restreint à n’introduire qu’un seul ruban pour chaque nœud. Nous nous poserons la question au chapitre VII de savoir si ce mode de concaténation peut être généralisé en ayant recours à plusieurs rubans entre chaque nœud, surtout dans les cas où nous disposons plusieurs ronds dans un nouage. Les tables de nœuds recensent les nœuds premiers et les chaînes premières définis ainsi grâce à ce mode de composition approximatif et assez amorphe algébriquement. Nous avons vu de manière interne à chaque objet, qu’une arithmétique plus riche est déjà à l’œuvre, et que de manière externe la composition des enlacements permet aussi, déjà, un calcul plus développé. Pour l’instant, avec notre description graphique, nous continuons à préciser les propriétés internes à nos objets. 1. Les nœuds coupures et les peignes Ce premier nœud dit le nœud trèfle est un nœud torique spécifique en tant qu’il est produit par un trajet régulier sur le tore2.
Avant d’étudier ces diverses présentations mises à plat, nous insistons sur cette présentation torique initiale. Elle justifie le nom qu’on lui donne. C’est la mise à plat de nœud qui présente le plus petit nombre de croisements. Remarquons que le plus petit nœud ne peut être réalisé qu’avec un minimum de trois croisements. Compte tenu du premier temps de notre algorithme, cette présentation correspond au plus petit nombre de vides. Sa surface d’empan minimum est ici un ruban de Mœbius à trois demi-torsions3. Il existe dans l’espace deux nœuds trèfles inverses l’un de l’autre au sens de l’inversion des dessus dessous à la hauteur des croisements. Ces deux nœuds trèfles ne sont pas superposables ou pour le dire autrement, il n’y a aucune série de mouvements de Reidemeister qui ne permette de transformer la mise à plat de l’un d’entre eux en la mise à plat d’un autre. Ce nœud peut être présenté comme bord d’une surface bilatère dans une autre présentation sur laquelle nous reviendrons plus bas. a2 - La famille des nœuds trèfles Ce nœud de trèfle initie une série de nœuds alternés :
Il s’agit de nœuds toriques qui accomplissent toujours deux tours longitudes et deux seulement, avec un nombre impair quelconque de tours méridiens4. Nous les comptons parmi les nœuds de trèfle. Ce sont les nœuds coupures car ils sont qualifiés grâce à nos coloriages par une coupure impaire.
Ces nœuds font partie des nœuds coupures. Les nœuds coupures sont des nœuds alternés dont tous les croisements sont traversés par la coupure. Ces nœuds coupures vont rentrer dans la composition des montages réguliers qui permettra de définir et de décrire un quelconque nœud. Il existe une configuration présentant seulement deux croisements. Dans ce cas, il ne s’agit pas d’un nœud propre mais d’une chaîne faite de deux ronds. Il y a l’enlacement simple à deux croisements qui est une chaîne torique.
Sur cette présentation de l’enlacement qui présente le plus petit nombre de croisements, nous pouvons tendre une surface d’empan grâce au premier temps de notre algorithme. Il y a alors deux pleins et deux vides.
Le deuxième temps de l’algorithme indique qu’il s’agit d’un non-nœud car il existe un coloriage qui ne nécessite pas de coupure. La surface d’empan minimum est un ruban orientable à deux demi-torsions. Il s’agit d’une sphère deux fois trouée et torsadée d’une torsion entière.
Notre propos consiste à opposer dans la structure ce qui est nœud, dont le nœud trèfle est la plus simple expression, et le non-nœud dont l’enlacement simple est l’exemplaire le plus réduit. a4 - La famille des enlacements toriques Ce premier cas se développe dans les enlacements élémentaires de deux ronds qui sont des chaînes.
Ils accomplissent, sur le tore, deux tours longitudes et deux seulement, et un nombre pair de tours méridiens.
Ce sont des non-nœuds puisqu’ils sont susceptibles d’un coloriage sans coupure.
Ces chaînes toriques sont dites ainsi parce qu’elles sont constituées de deux ronds du fait du nombre pair de tours méridiens sur le tore. Puisqu’il y a plusieurs ronds, il y a donc plusieurs coloriages. À changer le choix des couleurs sur un des ronds, le bi-coloriage d’un tel enlacement sans coupure, va présenter une coupure.
Ces chaînes toriques dont le nombre de croisements est pair vont servir de prototype dans les montages réguliers dans le cas des coupures passant par un nombre pair de torsions. Nous nous en servirons à ce titre dans la définition et la description des nœuds quelconques dans le chapitre suivant. Cette constatation ne contredit pas notre définition des non-nœuds puisque pour être dite telle parmi les objets alternés, il suffit qu’il existe un coloriage sans coupure. Nous appelons nœuds coupures, les nœuds toriques dont nous venons de parler qui ne font que deux tours longitudes, lorsque leur coloriage nécessite une coupure.
La présentation duale, définie au chapitre IV, d’un quelconque nœud coupure de la famille des trèfles ou de la famille des enlacements que nous venons de considérer, sont des peignes, impairs ou pairs.
Cette présentation duale est obtenue en inversant un arc périphérique de nos présentations toriques précédentes.
Nous appelons peignes, ces présentations duales des nœuds coupures, de la famille des enlacements et de la famille des trèfles. Ces peignes sont toujours susceptibles d’un coloriage sans coupure. Ce fait ne contredit pas notre distinction des trèfles comme nœuds coupures et des enlacements comme non-nœuds, car ces définitions prennent en compte la surface d’empan minimum de chaque objet, ainsi les présentations ayant le plus petit nombre de vides, ce qui n’est plus le cas des présentations duales.
Les peignes impairs ont comme bord un nœud de la famille des trèfles. Il n’y a donc qu’un seul coloriage sans coupure du fait qu’il s’agit d’un nœud propre. Par contre, les peignes pairs ont comme bord un enlacement qui est une chaîne de deux ronds. Il y a donc un autre coloriage qui cette fois présente une coupure.
Les peignes pairs et impairs sont obtenus comme le tressage de deux brins. Il s’agit de l’ensemble des tresses à deux brins qui sont refermées pour constituer des chaînes et des nœuds. Ces peignes pairs et impairs vont nous permettre de produire un quelconque non-nœud alterné. 2. Les non-nœuds et les pur-nœuds Nous étendons maintenant la description des objets en définissant le procédé qui permet d’obtenir respectivement à partir de peignes, la multiplicité des non-nœuds, et à partir des nœuds coupures, la multiplicité des pur-nœuds. Il s’agit des sections transverses qui sont de deux types, duales les unes des autres, les coupures transverses dans les non-nœuds et les bretelles transverses dans les purs-nœuds. L’existence de ces sections transverses provoque la véritable difficulté de la théorie des nœuds, comme nous l’annoncions en commençant. Sans elles, il n’y aurait que des tresses et la théorie des nœuds et des chaînes serait susceptible d’être ramenée à la théorie des tresses. La théorie des tresses peut être transcrite en théorie des groupes algébriques selon un procédé très simple. Ce résultat dû à Artin résout la question de leur classification. Coupures transverses Revenons aux peignes. Ce sont des objets alternés, présentant deux pleins et susceptibles d’un coloriage bicolore sans coupure. Si nous pratiquons des coupures transverses dans la surface d’empan d’un peigne, nous obtenons un non-nœud. Une coupure transverse est une coupure que l’on peut faire avec des ciseaux dans la surface d’empan. Une coupure transverse va toujours d’un vide vers un autre vide.
Les coupures transverses de peignes donnent des non-nœuds. Il est remarquable de noter que même les non-nœuds toriques (pairs), qui produisent pourtant des peignes par dualité, peuvent être obtenus pas sections transverses de peignes. Mais il faut rester attentif au fait que la torsion des croisements est inversée dans la dualité alors qu’elle reste inchangée dans ce procédé.
Le résultat qu’il importe de retenir, c’est qu’à l’inverse un non-nœud quelconque est toujours le produit de coupures transverses dans un peigne. Mais il va nous falloir le démontrer. Notons que les coupures transverses ne croisent jamais la coupure qui permet d’isoler les nœuds puisque nous les pratiquons exclusivement dans les non-nœuds. Bretelles transverses La notion duale des coupures transverses que nous pratiquons dans les non-nœuds est la bretelle transverse, c’est un ruban tendu en travers d’un vide dans un pur-nœud. Un jeu de bretelles ajouté à un nœud coupure donne un pur-nœud.
Notons à l’inverse des coupures transverses qui respectent toujours les coloriages si elles ne rencontrent pas la coupure que les rubans placés en travers des vides dans les pur-nœuds doivent respecter les coloriages à l’endroit de leur accrochage à la surface. Nous démontrons par dualité le même résultat que celui qui définit les non-nœuds comme pouvant toujours être obtenus par des coupures transverses dans les peignes. Ce résultat énonce alors qu’un pur-nœud peut toujours être obtenu par un jeu de bretelles transverses ajouté à un nœud-coupure. a2 - Les non-nœuds et les pur-nœuds Si un jeu de coupures transverses dans un peigne donne toujours un non-nœud, nous ne sommes pas assurés pour l’instant qu’un non-nœud est toujours obtenu à partir d’un peigne par un jeu de coupures transverses. Nous allons maintenant démontrer le résultat suivant. Un quelconque non-nœud est toujours obtenu d’un peigne par divers jeux de coupures transverses. Nous le démontrerons à l’inverse de ce que nous avons fait jusqu’à maintenant, en partant d’un non-nœud quelconque et en montrant qu’il donne toujours lieu à un peigne grâce à des rubans transverses.
Un non-nœud, en dehors du fait qu’il soit alterné, présente un ensemble de vides qui sont toujours de valence paire comme nous l’assure le principe déduit du deuxième temps de notre algorithme. Dans la présentation duale d’un croisement non-nœud, sans coupure, il passe une coupure si l’on ne change pas l’orientation des ronds correspondant au coloriage.
C’est dire qu’un croisement coupure est le dual d’un croisement non-coupure. Mais les zones vides d’un non-nœud étant de valence paire, nous pouvons relier ces différents croisements coupure de la présentation duale, de manière telle que la coupure forme un cercle.
En effet, la coupure entrant dans une zone de valence paire peut toujours sortir5 de cette zone. Enfin, il est remarquable que la coupure de la présentation duale d’un non-nœud se ferme en un cercle qui délimite dans le plan deux zones telles que l’une d’entre elles renferme et supporte toutes les zones d’une même couleur du non-nœud de départ6. Toutes les zones de l’autre couleur se trouvant de l’autre côté de la coupure, dans l’autre zone délimitée par le cercle formé par la coupure. De ce fait, démontré à partir de notre algorithme qui établit la parité des zones vides d’un objet se présentant comme un non-nœud, nous pouvons toujours réunir par des rubans monochromes sans torsion ne rencontrant pas la coupure en question, le jeu des zones d’une même couleur pour les transformer en une seule zone. Il en est de même des zones de l’autre couleur.
Ces rubans, réunissant les zones monochromes de part et d’autre du cercle de la coupure dans le dual, ne se croisent pas, ne s’encombrent pas, ne se font pas d’obstruction mutuelle du fait qu’ils transforment ces zones de valence paire en autant de zones de valence deux.
Nous pouvons conclure qu’il est toujours possible de reconstituer un peigne qui ait une surface d’empan présentant exclusivement deux pleins et des vides de valence deux, dont le nombre de croisements est égal à celui du non-nœud donné. Nous avons donc démontré le résultat que nous annoncions. Nous effectuons la même transformation dans un cas plus riche, c’est-à-dire plus compliqué en apparence, mais qui présente la même simplicité, car la même propriété de structure.
Cette propriété de structure se voit encore mieux au point de paraître triviale si nous effectuons la transformation inverse produisant un non-nœud à partir d’un peigne en présence de la coupure dans le dual.
Le lecteur remarquera pourtant que nous n’avons pas effectué ici les coupures transverses qui annulent exactement les bretelles ajoutées dans la présentation de la transformation inverse des figures 25, 28 et 29. De ce fait, la coupure tracée dans le dual du non-nœud considéré ne parcours pas les vides selon le même trajet. Cela montre qu’il y a lieu de se plier à un calcul sur les dessins qui n’est pas trivial. Si nous voulons obtenir le trajet précédent de la coupure, il faut couper le peigne de manière différente.
Le résultat dual s’énonce ainsi, un quelconque pur-nœud peut toujours être obtenu par des rubans transverses à partir d’un nœud coupure. En effet, un pur-nœud est un objet tel que la coupure passe par tous les croisements.
Nous pouvons toujours reconstituer un nœud coupure à partir d’un pur-nœud par autant de coupures transverses qu’il le faut et ne rencontrant pas la coupure.
Ces coupures transverses ne sont que des rubans transverses ajoutés au non-nœud dual comme dans la démonstration précédente. Ainsi, le résultat dual annoncé, un quelconque pur-nœud peut toujours être obtenu par des rubans transverses à partir d’un nœud coupure.
Maintenant que nous savons décrire tous les non-nœuds et tous les pur-nœuds à partir des peignes et des nœuds coupures, grâce aux sections transverses, nous pourrons montrer dans le chapitre suivant, comment les objets alternés quelconques dont nous voulons faire la théorie sont obtenus à partir de ces éléments grâce à un mode de composition régulier. Il nous suffira de pratiquer ces sections transverses sur des montages réguliers réalisés à partir des peignes et des nœuds coupures exclusivement. De ce fait nous appellerons montages réguliers ces composés construit exclusivement à partir de peignes et de nœuds coupures. II. Plasticité nodale Les objets non alternables respecteront ces bâtis (univers). Ces bâtis correspondent aux immersions dans le plan, quoiqu’ils posent un problème plastique et topologique plus large et non seulement graphique. Les objets non alternables représentent une difficulté supplémentaire puisque le nœud accomplit une non-alternabilité que nous résoudrons du point de vue nodal. L’étude arithmétique des chapitres précédents commence à en rendre raison. Dans cette approche plastique, la source de nos objets est différente puisque les mouvements de la théorie des Enlacements permet de réalterner un objet quelconque présentant un, deux ou trois ronds et même au-delà comme nous le montrons maintenant. La théorie des enlacements devient théorie des non-nœuds de un à trois ronds. Nous prolongerons l’arithmétique des nœuds dans le chapitre suivant lorsque nous aurons achevé la description graphique des bâtis qui suivent les présentations alternées. 1. Théorie des non-nœuds de un à trois ronds Nous appelons non-nœud, un nœud ou une chaîne alternée dont la surface d’empan minimale est bicolorable, c’est-à-dire qui ne nécessite pas de coupure. Ces non-nœuds sont toujours alternés par définition. Nous pouvons parler d’une théorie des non-nœuds à l’occasion de la théorie des Enlacements dans les cas constitués de un, deux ou trois ronds. Sous cette condition portant sur le nombre de ronds, r £ 3, sachant que toutes les présentations de nœuds et de chaînes alternées et non alternées appartiennent à un Enlacement, nous appelons maintenant cette classe un non-nœud, car nous pouvons avancer : L’existence des non-nœuds standard Chaque classe, constituant ce que nous avons appelé un Enlacement, possède un non-nœud standard qui la représente. Ce fait est démontré par l’étude formelle des répartitions d’enlacements par le tableau caractéristique des états d’enlacements, du mouvement des signes négatifs qui marquent le changement d’orientation de ronds aussi bien que l’inversion des signes caractéristiques des croisements dans le formalisme que nous avons introduit dans l’étude des relations Renl et RS et la construction effective des non-nœuds. Donnons, pour r £ 3, les deux tableaux présentant la plus riche complication dans ce domaine. Les états d’enlacements plus simples sont obtenus lorsque certaines valeurs de ces tableaux sont nulles ou certaines lettres absentes :
Nous savons construire, comme nous allons le montrer immédiatement, un exemplaire de chaque état d’enlacement correspondant à chaque tableau donc à chaque non-nœud. Cet exemplaire offre dans chaque cas un nombre minimum de croisements et il est purement impropre. Nous appelons ce non-nœud représentant une classe donnée, le non-nœud contenu S0 dans une quelconque présentation appartenant à cette classe. a1 - Construction des non-nœuds de un à trois ronds contenus dans un nœud ou une chaîne Un - Commençons par les nœuds constitués d’un seul rond. Il n’y a qu’un seul non-nœud, c’est le nœud trivial :
Deux - Dans le cas des chaînes faites de deux ronds, à part la chaîne triviale :
Les non-nœuds sont constitués par la série des non-nœuds toriques de torsion positive :
Trois - Dans le cas des chaînes faites de trois ronds, à part la chaîne triviale et les enlacements précédents accompagnés d’un rond libre, les non-nœuds sont constitués par les chaînettes alternées de torsion positive faites de trois ronds :
et les deux séries des chaînes olympiques inverses l’une de l’autre, dont nous donnons les premiers exemplaires :
Ces deux séries différentes se résument dans les figures suivantes indexées par trois nombres entiers :
Nous avons fixé ici la présentation prototypique représentant chaque non-nœud de notre théorie sous l’aspect d’un non-nœud standard. Nous obtenons bien tous les types modulo R0 et RS. a2 - Un autre calcul de l’enlacement Pour une présentation donnée, r £ 3, nous construisons l’état d’enlacement qui en fait partie, sous l’aspect de son non-nœud standard. Aux répartitions de ces enlacements correspond une répartition des nombres de chaîne qui nous permet de désigner ce non-nœud standard de cet état de l’enlacement. Nous pouvons dès lors parler du non-nœud S0 contenu dans un nœud ou une chaîne. La moyenne des nombres de coupure S0 du non-nœud contenu S0 de la classe d’équivalence de la présentation donnée fournit un nouveau calcul de l’enlacement contenu dans la chaîne en fonction de la torsion, indépendamment des coloriages. Soulignons que les non-nœuds standard contenus dans les chaînes sont purement impropres et que par conséquent un calcul simple s’impose. Opposition des nombres duaux de coupure moyenne Pour les non-nœuds standard, la moyenne des nombres de la coupure calculée dans le dual S*0 est l’opposée de la moyenne des nombres de la coupure S0, soit : S*0 = –S0 Dans les non-nœuds standard, la vrille propre est nulle, h = 0, car il n’y a pas de croisement propre. Ainsi d’après notre théorème principal : C0 – 2S0 = 0 C*0 – 2S*0 = 0 Or l’égalité C*0 = –C0 se trouve justifiée du fait de l’inversion des signes de torsion dans la dualité, d’où notre proposition. Mais ce changement de signe n’a aucun effet sur la définition du nombre caractéristique de l’enlacement ainsi calculé, si nous nous en tenons aux présentations en non-nœuds constructions proposées. Seule une des séries olympiques présente des nombres négatifs de l’enlacement. Ceci tient au fait de l’existence des deux tableaux dans les seuls cas où tous les nombres d’enlacement sont non nuls. 2. Théorie des enlacements à partir de quatre ronds Au-delà de trois ronds, nous savons encore construire des exemplaires de certaines des répartitions des enlacements. Il leur correspond un état de l’enlacement rendu par un tableau seulement plus étendu que dans les cas de moins de trois ronds :
Ce tableau correspond à cette présentation alternée.
Ces exemplaires se présentent comme des non-nœuds, ils offrent le nombre minimum de croisements alternés et sont purement impropres, ils sont ainsi alternables. À partir de ces bâtis, nous savons construire des exemplaires des autres états de l’enlacement. Lorsqu’ils ne sont pas réalternables, le tableau de la répartition ne comporte aucune ligne entièrement positive ou négative. L’existence de ces cas non alternables qui ne peuvent par conséquent pas être représentés par un non-nœud, est attesté par un calcul. Cette existence tient à une contrainte combinatoire qui s’impose dans la répartition des signes positifs et négatifs. Ils se présentent sans coupure mais ils sont non alternés, et ils offrent le nombre minimum de croisements si ceux-ci sont comptés en valeur absolue indépendamment des orientations. Ils sont purement impropres. En voici un exemple :
accompagné du tableau de son état d’enlacement.
Or nous pouvons construire grâce à des mouvements gordiens des exemplaires réalternés de ces états variés d’enlacements. Ils présentent une coupure dans ce cas du fait de l’alternance et ces prototypes ne sont donc pas des non-nœuds. Ils offrent le nombre minimum de croisements alternés et sont purement impropres. À l’occasion du cas précédent, nous obtenons par exemple la présentation alternée suivante.
Nous appellerons présentations minimales alternées ce type d’exemplaire. Par conséquent, nous pouvons construire des exemples de chaque état d’enlacement. À partir de quatre ronds, il y aura deux non-nœuds et des cas non alternés sans coupure, ces derniers pouvant être réalternés moyennant une coupure. Ce fait justifie que nous ne puissions pas parler d’une théorie des non-nœuds pour la théorie des enlacements lorsque le nombre de ronds est supérieur ou égal à quatre. Mais nous obtenons ainsi, dans tous les cas, des présentations alternées de répartition de nombres d’enlacements que nous choisissons comme cas exemplaire de la répartition. À partir de quatre ronds, le nœud n’est plus un accomplissement de coupure puisque c’est aussi le cas de certains états d’enlacements. Il y a donc là une différence entre trois et quatre, puisque tous les cas exemplaires d’ordre inférieur ou égal à trois sont des non-nœuds (alternés), et que le premier cas exemplaire alterné présentant une coupure nécessaire apparaît à l’ordre quatre. 3. Retour à la théorie de la dimension et à l’accomplissement de la coupure La présence nécessaire de la coupure à partir de quatre ronds, dans les présentations alternées exemplaires de certains états d’enlacements, est une indication liée à la dimension de l’espace dans lequel les ronds sont plongés. Travaillant en dimension trois, un effet d’encombrement se produit à partir de quatre ronds. La dimension de l’espace Ceci donne lieu à une nouvelle définition de la dimension de l’espace. Un espace est dit de dimension trois lorsqu’à partir de quatre ronds (de dimension un chacun) il n’admet plus une théorie des non-nœuds. Ceci peut être dit encore autrement, en rapprochant ce fait de l’impossibilité de plonger le plan projectif dans l’espace de dimension trois. Nous pouvons considérer la coupure nécessaire à la réalternance des chaînes à quatre comme une singularité, qui révèle un nœud, analogue à la ligne d’immersion ou au trou dans les surfaces non orientables. En effet, nous savons immerger ces surfaces non orientables en dimension trois, moyennant une ligne de points multiples, dite ligne d’immersion; c’est le cross-cap, par exemple :
Ou nous savons aussi les plonger dans l’espace de dimension trois, moyennant un trou imaginable comme rupture de surface, c’est la bande de Mœbius si nous conservons ce même exemple. Dans le cas du plan projectif, un trou le transforme en bande de Mœbius. La ligne d’immersion ou ce trou de plongement, sont des singularités caractéristiques nécessitées par la représentation de ces surfaces en dimension trois. Cette remarque peut être rapprochée d’une nouvelle fonction de la coupure accomplie par le nœud jusqu’à trois ronds. La première fonction du nœud, révélée par la coupure, produit la multiplicité des plongements des enlacements quel que soit le nombre de ronds. Cette fonction existe encore en dimension trois plus un, comme le prouvent les chaînes qui ne se défont pas par homotopies, mais elle y est plus réduite. Ceci nous est accessible car la théorie des nœuds et des chaînes à homotopie près en dimension trois est un modèle de la théorie de ces objets en dimension quatre. Ainsi la nouvelle fonction de la coupure assure le plongement de certains enlacements à partir de quatre ronds en dimension trois. Nous en voulons pour preuve le fait que l’accomplissement de la coupure se glisse déjà à partir de trois ronds dans la présentation duale des non-nœuds, alors que les non-nœuds de deux ronds ne nécessitent même pas, non plus, de coupure dans la présentation duale. Comme quoi le nœud révélé par la coupure commence à apparaître, dans le dual des non-nœuds, à partir de trois. De la même manière, à partir de deux ronds, les chaînes sans coupure contenant du nœud voient toujours celui-ci se défaire par homotopie. Ces chaînes sont aussi des non-nœuds, mais ne sont pas standard. Nous préciserons à la fin de cet ouvrage dans quelle théorie cette singularité disparaît. Le nombre de ronds et l’accomplissement de la coupure sont en raison inverse. En théorie des surfaces les deux singularités remarquable de la présentation du plan projectif sont : — d’une part la ligne d’immersion nécessitée par cette immersion (cross-cap), ou le trou nécessitée par le plongement (bande de Mœbius).
— d’autre part la ligne sans point7 caractéristique de la structure. Ainsi en théorie du nœud, ces deux singularités remarquables de la présentation du plan projectif se trouvent homogénéisées par la coupure de la surface d’empan des chaînes à partir de quatre ronds. Il est bien évident que ceci mérite d’autres développements, puisque voici située dans notre présentation la principale raison qu’a rencontrée Lacan pour passer des surfaces topologiques intrinsèques au nœud. Cette raison touche à l’homogénéisation de la fonction phallique, à l’horreur de la castration par opposition à sa représentation. Nous reprendrons ces questions par la suite, mais en renvoyant dès maintenant à la théorie des chaînes en dimension quatre (codimension trois), étudiée par Milnor et explorée par P. Soury dans le cas d’une théorie en dimension trois admettant la seule homotopie en plus des mouvements de Reidemeister (TH) et aux travaux de M. Bertheux qui a amplifié l’ensemble de leurs résultats. e1 - Les non-nœuds comme coupures de peignes Quel est le nœud obtenu par les coupures du 4-peigne suivant :
Changez la présentation du dernier dessin. À partir de ce résultat, dire la relation qu’entretiennent ces 2-chaînes, en termes de coupures de peigne.
Pouvez-vous trouver la relation entre ces 2-chaînes en termes de coupures de peigne?
Généralisation, de quel peigne procède ce non-nœud, par quelles coupures transverses?
e2 - Les pur-nœuds comme nœuds coupures raccordés par des bretelles. Quelle relation entretiennent ces deux nœuds?
© 1999 Topologie En Extension . Tous droits de reproduction et de représentation réservés. Tous les textes, dessins et graphiques reproduits dans cet ouvrage sont protégés par des droits de propriété intellectuelle détenus par Topologie En Extension. Par conséquent, aucun de ces éléments ne peut être reproduit, modifié, transmis, rediffusé, traduit, vendu, exploité commercialement ou réutilisé de quelque manière que ce soit sans l'accord préalable écrit de Topologie En Extension. |

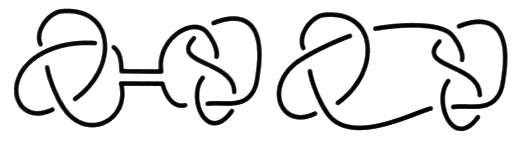
 Fig. 3
Fig. 3 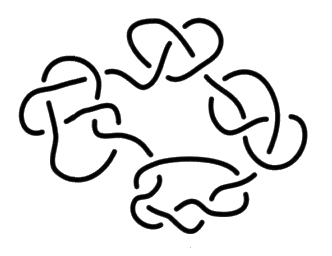 Fig. 4
Fig. 4 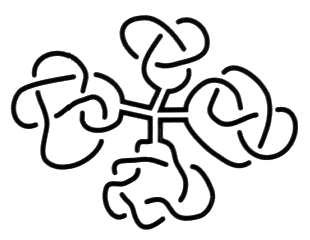 Fig. 5
Fig. 5 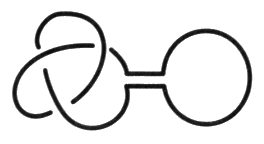 Fig. 6
Fig. 6 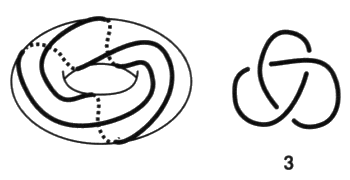 Fig. 7
Fig. 7 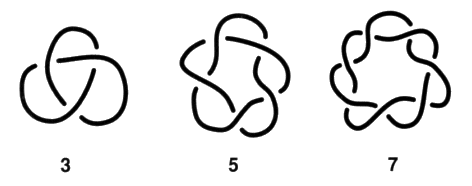 Fig. 8
Fig. 8 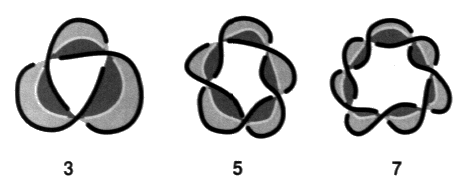 Fig.
9
Fig.
9  Fig. 10
Fig. 10  Fig. 11
Fig. 11  Fig. 12
Fig. 12 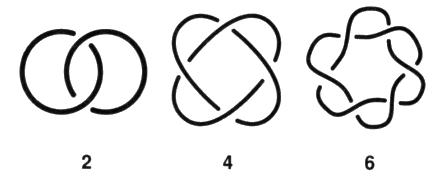 Fig. 13
Fig. 13 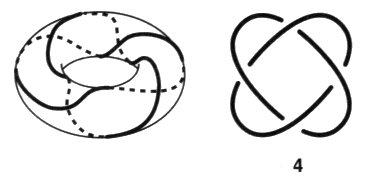 Fig. 14
Fig. 14 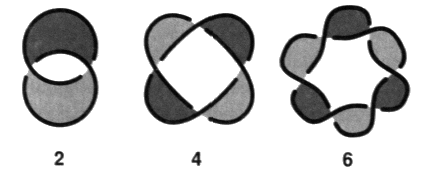 Fig. 15
Fig. 15 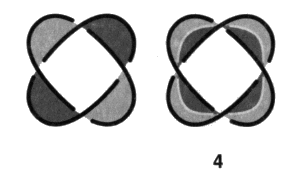 Fig. 16
Fig. 16 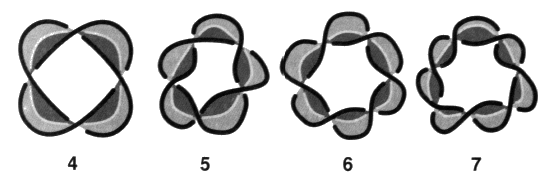 Fig. 17
Fig. 17  Fig. 18
Fig. 18  Fig. 19
Fig. 19 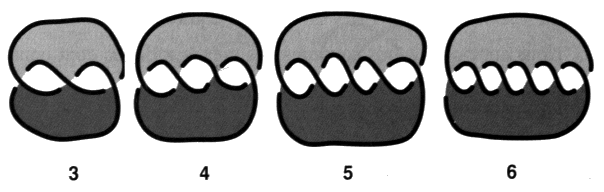 Fig. 20
Fig. 20 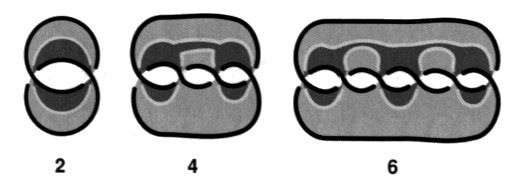 Fig. 21
Fig. 21 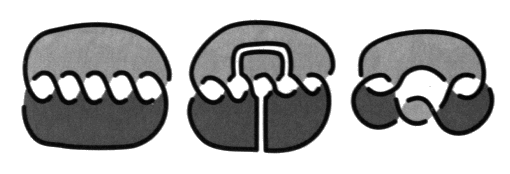 Fig. 22
Fig. 22 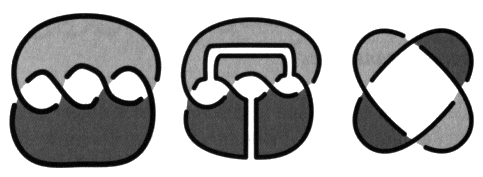 Fig. 23
Fig. 23 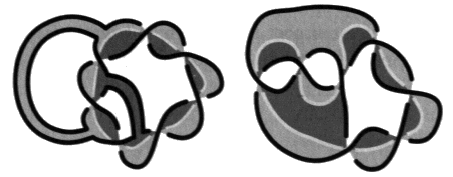 Fig. 24
Fig. 24 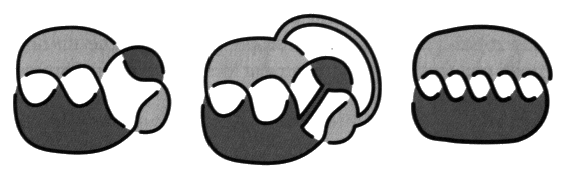 Fig. 25
Fig. 25 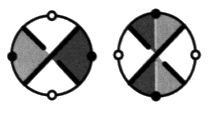 Fig. 26
Fig. 26 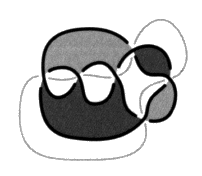 Fig. 27
Fig. 27 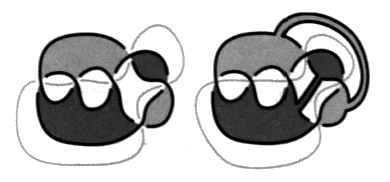 Fig. 28
Fig. 28 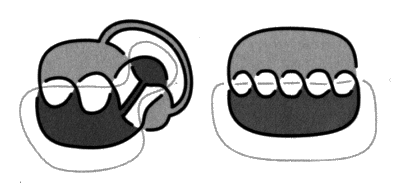 Fig. 29
Fig. 29  Fig. 30
Fig. 30 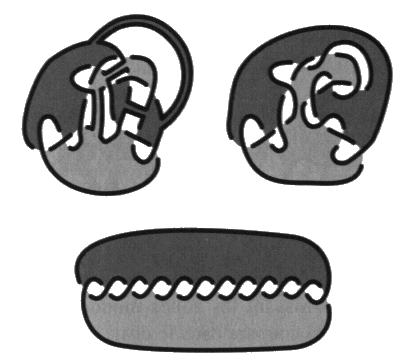 Fig. 31
Fig. 31 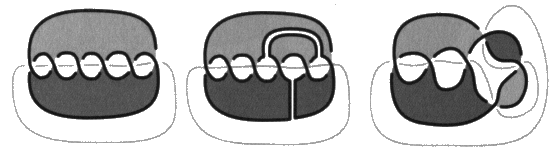 Fig. 32
Fig. 32 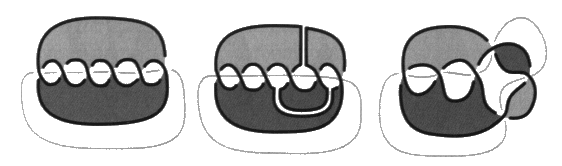 Fig. 33
Fig. 33  Fig. 34
Fig. 34  Fig. 35
Fig. 35 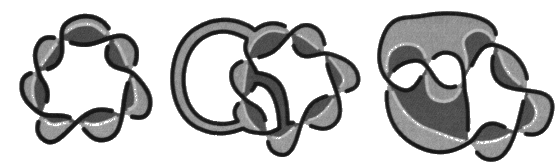 Fig. 36
Fig. 36  Fig. 37
Fig. 37  Fig. 38
Fig. 38 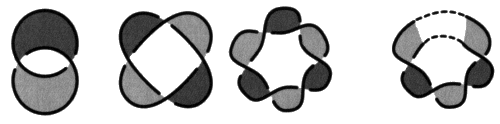 Fig. 39
Fig. 39 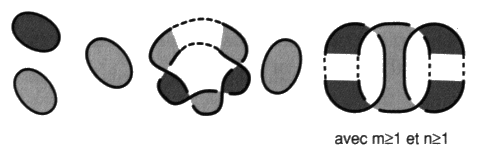 Fig. 40
Fig. 40  Fig. 41
Fig. 41 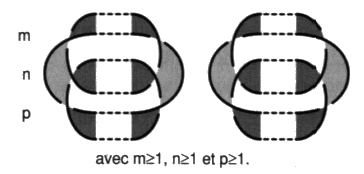 Fig. 42
Fig. 42 
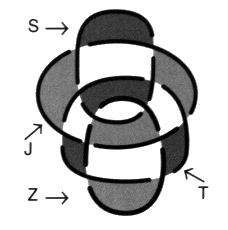 Fig. 43
Fig. 43 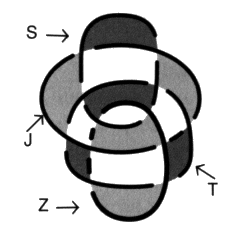 Fig. 44
Fig. 44 
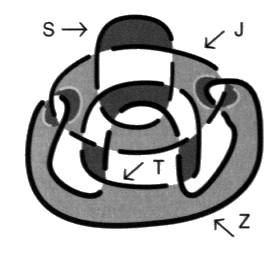 Fig. 45
Fig. 45 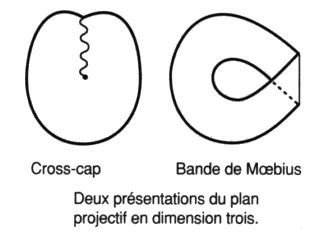 Fig. 46
Fig. 46 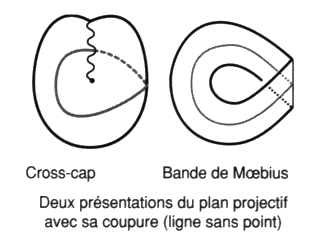 Fig. 47
Fig. 47  Fig. a
Fig. a  Fig. b
Fig. b 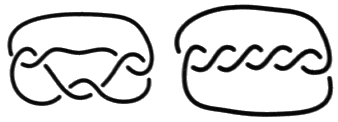 Fig. c
Fig. c  Fig. d
Fig. d 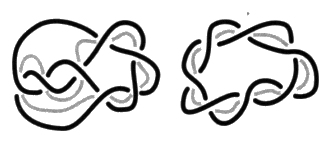 Fig. e
Fig. e