Éléments pour une théorie de la représentation et de l’objet

Le fait d’étendre de la couleur pour en badigeonner des zones n’est pas un geste trivial comme il pourrait paraître à un esprit pressé. Si nous comparons ce coloriage à ce qu’exige un semblant de calcul, comme le fait d’orienter des cycles, nous sommes surpris par la traduction exacte qui insiste entre les résultats de ces activités bien différentes en apparence.

Leur différence tient à la dimension, deux pour l’aplat coloré, un pour les trajets orientés.

Nous sommes tenté de croire que la surface étendue se prête plus à la représentation et à la ressemblance propre à l’analogie, la ligne tracée à l’écriture et à la signification impropre à la métaphore. Pourtant, ici, nous allons montrer qu’elles se croisent en une traduction stricte.

1. Le coloriage

Nous n’y insisterons pas plus ici, puisque le coloriage est l’objet principal de notre premier geste dans l’investigation du nœud. Soulignons simplement que l’effet de la couleur étendue dans les zones reste qu’elle marque, après avoir établi la distinction entre pleins et vides, les éléments de ficelle d’un coté par une couleur. Il y a donc deux couples différentiels premiers dans ce procédé, à la fois sombre/clair, et d’autre part droite/gauche.

Pour un élément de ficelle unique en son cas:

Cela donne quatre cas colorés:

Nous voulons comparer ce quatuor au couple d’orientations de l’élément de corde.

2. L’orientation

Nous le signalions dès le début, un élément de ficelle prélevé dans un cycle est susceptible de deux orientations, ici vers le haut ou vers le bas.

3. La traduction

Elle repose sur une équivalence proposée entre les indicateurs précédents qui se composent en respectant cette relation:

Pour le coloriage, le changement sombre/clair ou le changement droite/gauche équivaut selon ce principe de traduction à un changement d’orientation haut/bas. Un double changement ramène à la situation initiale.

Nous pouvons établir cette correspondance grâce à deux cycles de base qui la condensent en deux petits dessins:

4. Accumulation

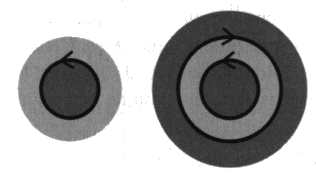
Nous constatons alors que cette façon de faire est cohérente avec une série de cercles concentriques alternativement orientés selon l’une ou l’autre des deux orientations:

Et que cette façon de faire est aussi cohérente avec les sections transverses que nous sommes susceptibles de produire entre ces cercles orientés:

Ces sections transverses respectent la composition entre elles des orientations des cycles.

Nous pouvons même généraliser cette pratique des coloriages et des orientations à des cercles concentriques diversement orientés. Mais il faut alors ajouter aux coloriages un troisième élément sous l’aspect d’une coupure qui fait bord entre les couleurs. Nous appelons bord qui consiste ce type de cycles coupures.

Les sections transverses ne peuvent pas franchir ce bord qui consiste, car elles ne respecteraient plus alors les orientations de cycles. Mais ce bord est susceptible lui-même d’une orientation.

Ces coloriages et cette coupure restent cohérents avec les sections transverses si nous ajoutons des sections tordues entre les cercles. C’est dire que nous pouvons considérer les cycles de départ comme des cercles de Seifert.

Nous pouvons aussi ne tenir compte que d’un coloriage de zones sur deux en introduisant la notion de zones pleines et de zones vides.

Notre étonnement reste entier devant la cohérence de cet ensemble de faits, sachant qu’avec des principes de coloriages bien définis, nous pouvons faire l’économie des orientations des cycles qui restent là déterminés univoquement en fonction du choix de cycles de base donnés.