Nous nous proposons d’utiliser l’expression suivante où x Î Z₂ et y Î Z₂ :

1. Les éléments

Une quelconque configuration peut être décomposée par un graphe (dit graphe de Terrasson) en des pièces de deux types, et de deux types seulement, nous les appellerons poinçons générateurs.

Nous désignons les deux poinçons générateurs par les valeurs :

et formulons les deux modes de composition dans le cas de poinçons plus généraux.

a1 - Forme générale du poinçon

Un poinçon a la forme générale suivante :

où V (m, n) = l^m rⁿ désigne le nombre de ronds constitués à l’intérieur du poinçon avec m Î N et n Î N, et :

a2 - Les poinçons générateurs

Les poinçons générateurs sont donc bien :

2. Les compositions

Les lois de composition des poinçons s’écrivent alors ainsi.

a1 - La composition par les pleins

Pour la composition par les pleins :
 

	P (x, m, n) Ù P (x’, m’, n’) = B (x") . V (m", n")
où	B (x") = F (x Ú x’, 0)
et	V (m", n") = F (x Ù x’, 0) . V (n, m) . V (n’, m’)

Soit :

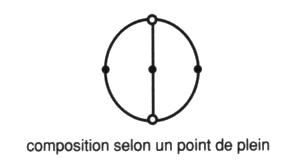
a2 - La composition par les vides

Pour la composition par les vides :
 

	P (x, m, n) Ú P (x’, m’, n’) = B (x") . V (m", n")
où	B (x") = F (x Ù x’, 0)
et	V (m", n") = F (x Ú x’, 1) . V (m, n) . V (m’, n’)

Soit :

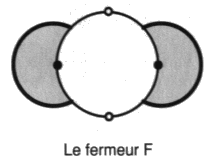
a3 - Le fermeur

Enfin, le fermeur introduit un facteur multiplificateur :

3. Exemples

a1 - Deux poinçons (a’)

La composition par les pleins de deux poinçons (a’) ajoute un rond de plein :

Nous composons deux poinçons P (1, 0, 0) sachant que :
 

	P (1, 0, 0) = f (1, 0) . V (0, 0) = f (1, 0) = l.
	P1 (x", m", n") = P (1, 0, 0) Ù P (1, 0, 0) = B (x") . V (m", n")
où	B (x") = f (1 Ú 1, 0) = f (1, 0) = l
et	V (m", n") = f (1 Ù 1, 0) . V (0, 0) . V (0, 0) = f (1, 0) = l
ainsi:	P1= P (1, 1, 0) = f (1, 0) . f (1, 0) = l2

et devient, si nous lui ajoutons un fermeur :

Nous laissons au lecteur le soin de vérifier que P₁ muni d’un fermeur présente bien trois cercles entourant des zones pleines.

a2 - Deux poinçons (a)

Par contre, la composition par les vides de deux poinçons (a) ajoute un rond de vide :

Nous composons deux poinçons P (0, 0, 0) sachant que :
 

	P (0, 0, 0) = f (0, 0) . V (0, 0) = f (0, 0) = 1
	P2 (x", m", n") = P (0, 0, 0) Ù P (0, 0, 0) = B (x") . V (m", n")
où	B (x") = f (0 Ú 0, 0) = f (0, 0) = 1
et	V (m", n") = f (0 Ù 0, 1) . V (0, 0) . V (0, 0) = f (0, 1) = r
ainsi:	P2 = P (0, 0, 1) = f (0, 0) . f (0, 1) = r

Ceci devient si nous lui ajoutons un fermeur :

Nous laissons ici encore le soin au lecteur de vérifier que P₂ muni d’un fermeur présente bien deux cercles, l’un entourant une zone pleine et l’autre entourant une zone vide.

Principe de lecture

Le principe à adopter pour lire le résultat sur la figure est le suivant : Nous lisons l et r pour chaque cercle selon qu’il enserre un plein ou un vide.

L’action du fermeur peut être décrite par la formule :

qui écrit le constat suivant que le fermeur achève toujours un rond enserrant un plein dans le poinçon.

a3 - L’objet petit a aux Chinois

a4 - L’exercice proposé

Nous pouvons formaliser la solution de l’exercice proposé :

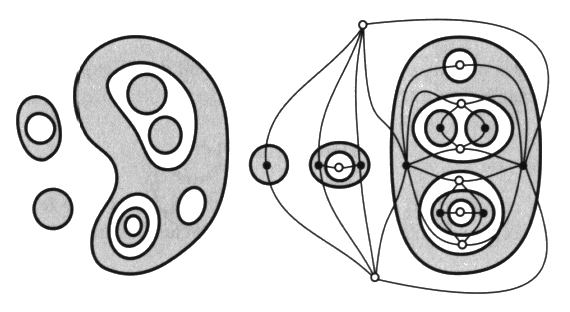
Nous pouvons décrire linéairement cette solution bien qu’elle se dessine dans les deux dimensions du plan.

Nous marquons par des parenthèses grasses le changement de direction dans le dessin. Nous avons choisi de mettre le graphe sur une présentation qui fait apparaître ce changement de direction dans la composition. Il équivaut à l’échange des signes de composition Ù et Ú.

Nous opérons les premiers regroupements lisibles sur la figure :

Grâce à cela, nous trouvons mieux les césures correspondant aux parenthèses et au changement de direction dans le dessin :

Effectuons le regroupement le plus important à droite de la figure et commençons à exprimer les poinçons obtenus en termes de bord et de nombres de cercles :

Nous obtenons en fait le poinçon suivant dont l’expression est lisible sur la figure :

Il contient cinq cercles de chaque sorte et qui avec le fermeur donne six cercles entourant un plein et cinq cercles entourant un vide :

Nous avons utilisé la forme générale du poinçon :

qui à la fin avec le fermeur ne se distingue plus :

© 1999 Topologie En Extension . Tous droits de reproduction et de représentation réservés. Tous les textes, dessins et graphiques reproduits dans cet ouvrage sont protégés par des droits de propriété intellectuelle détenus par Topologie En Extension. Par conséquent, aucun de ces éléments ne peut être reproduit, modifié, transmis, rediffusé, traduit, vendu, exploité commercialement ou réutilisé de quelque manière que ce soit sans l'accord préalable écrit de Topologie En Extension.