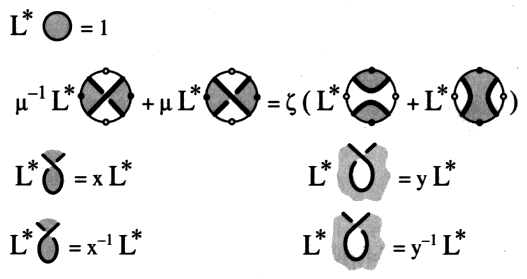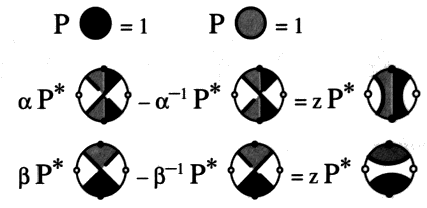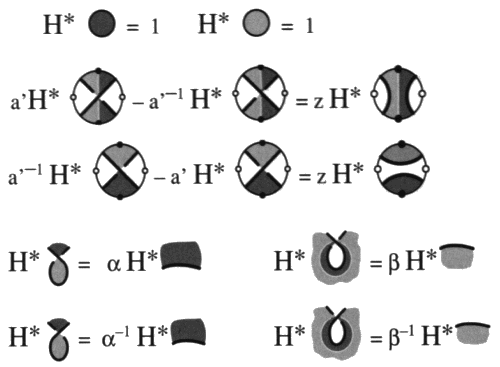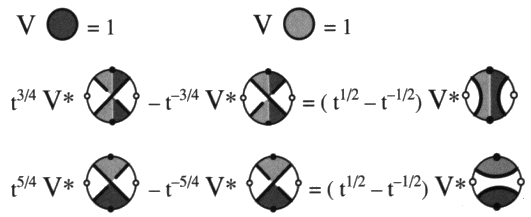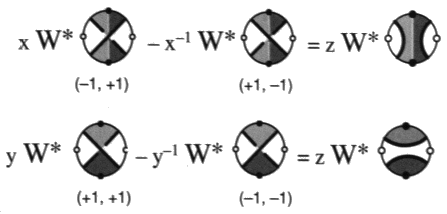Chapitre III Polynômes L’entrée dans les calculs de polynômes de nœuds et de chaînes se fait sûrement le plus simplement par le polynôme de L. Kauffman. Nous suivons ce mathématicien dans [18. d et c]. 1. Du polynôme de Kauffman au polynôme de Jones Ce calcul nécessite une décomposition par lissage de l’objet comme en chaque cas, depuis Conway, lorsqu’il s’agit de calcul d’entrelacs (Skein Calculus) afin d’obtenir un de ces polynômes. 1 - LissageIl s’agit de décomposer chaque croisement de l’objet en deux lissages :
Chaque lissage est pourvu d’un indice. Donnons un exemple d’une telle décomposition, en prenant l’exemple du nœud de trèfle :  Fig. 2 Fig. 2
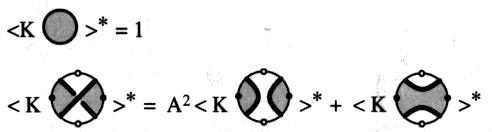
Chaque état s résultant de la décomposition de K, présente un produit des indices des lissages successifs et un certain nombre de ronds. 2 - Le bracket polynômeDonnons l’expression du bracket-polynôme construit par Kauffman < K > d’un objet donné K :
où < K | s > désigne le produit des indices attachés à s, et ||s|| désigne le nombre de ronds de s, diminué de un, et posons que : d = ( – A 2 – A–2)Ce polynôme est donc une combinaison linéaire de la lettre d à la puissance du nombre de rond de chaque état, moins un — c’est dire que ce nombre est diminué d’une unité — combinaison dont les coefficients sont les produits des indices de chaque état. Il est à noter que le bracket-polynôme de Kauffman est établi dans le cas d’un objet non orienté quant aux ronds. C’est un invariant de chaînes et de nœuds non orientés à isotopies régulières près. C’est dire qu’il est sensible aux boucles (B1). À partir de ce polynôme, il est aisé d’en obtenir d’autres auxquels correspondent parfois différents calculs d’entrelacs (Skein Calculus), mais ce n’est pas toujours le cas. 3 - Son calcul d’entrelacsLui-même est le produit d’un calcul d’entrelacs qui autorise la définition que nous avons donnée. À partir du polynôme du nœud trivial : < K Le lissage peut être rendu par la formule : < K 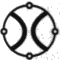 > >
C’est ce que nous appelons un calcul d’entrelacs (Skein calculus). Passons au polynôme correspondant à l’isotopie d’ambiance déduit du bracket polynôme de Kauffman. 4 - Le polynôme régularisé du polynôme de KauffmanCe polynôme est un invariant des objets orientés quant aux ronds à isotopies d’ambiances près. Il ne lui correspond pas de calcul d’entrelacs : L K (A) = ( –A3)–v(K) < K > (A)où v(K) est la vrille — la somme de la caractéristique de tous les croisements — de l’objet K. C’est une étape nécessaire pour atteindre le polynôme de Jones. 5 - Le polynôme de JonesLe polynôme de Jones a été obtenu par une voie indépendante du bracket polynôme, mais il s’obtient du précédent par un changement de variable. Si nous posons : A = t –1/4nous obtenons le polynôme de Jones : V K (t) = LK (t–1/4)Ce polynôme est l’objet d’un calcul d’entrelacs, nous le donnerons plus loin. Son mérite est de distinguer les deux nœuds trèfles, par exemple. Il a donné l’occasion de construire le polynôme de Homfly qui n’est que le polynôme de Jones à 2 variables et qui par contrecoup a fait voir son intérêt aux lecteurs du Bulletin de la société américaine de mathématique. Eux-mêmes ne s’en n’étaient pas rendu compte avant que quatre équipes différentes de mathématiciens aient produites en même temps le polynôme de Homfly. Nous signalons cette anecdote dans l’histoire des publications scientifiques aujourd’hui, pour la valeur indicative qu’elle a de l’état de la communication scientifique. Il y a une véritable difficulté de lecture et les fanfaronnades ne servent à rien pour cacher l’incapacité à assumer cette domination de la lettre dont les sujets sont les marionnettes dans la réalisation industrielle. 2. Le polynôme semi-orienté à 2-variables (polynôme de Kauffman) Nous pouvons rapporter le polynôme de Jones à un autre polynôme ayant trait aux objets orientés quant aux ronds. N’étant pas directement obtenu par un calcul d’entrelacs, il provient d’un polynôme susceptible d’un tel calcul. 1 - Le polynôme LK et son calcul d’entrelacsNous le graphématisons par : L K (n, z)Il est invariant à l’isotopie régulière près, voici les éléments nécessaires à son calcul : 2 - Le polynôme semi-orienté à 2-variables FK (polynôme de Kauffman) C’est le polynôme régulier du polynôme L K :F K (n, z) = n–v(K) LK (n, z)où v(K) est toujours la vrille de l’objet K. 3 - CorrespondancesLe bracket-polynôme de Kauffman est un cas particulier de L, et le polynôme de Jones un cas particulier de F du polynôme de Kauffman. K ( –A3, A + A–1) avec : n = –A3 z = A + A–1 et : V K (t) = FK (– t-3/4, t–1/4 + t1/4)avec : n = –t-3/4 z = t–1/4 + t1/4Ces changements de variables donnent la relation rencontrée plus haut dans le changement de variable : A = t –1/43. Le polynôme de Jones et ses dérivés Nous disposons déjà d’un moyen de calculer le polynôme de Jones à partir du calcul du bracket-polynôme de Kauffman : V K (t) = LK (t–1/4)Mais il est susceptible d’un calcul d’entrelacs. 1 - Calcul d’entrelacs pour le polynôme de JonesVoici les formules nécessaires à ce calcul :
Grâce à ces deux équations nous pouvons calculer ce polynôme à partir de la figure, en la décomposant par inversions et lissages successifs. a2 - Le polynôme orienté à 2-variables (Homfly) et son calcul d’entrelacs Il s’agit du polynôme : P K (a, z)obtenu par le calcul de sa décomposition grâce à la formule :
Il correspond par le changement de variable suivant :
au polynôme de Jones :
et par le changement de variable plus simple : a = 1 au polynôme d’Alexander-Conway : Ñ K ( z) = PK ( 1, z) 3 - Le polynôme d’Alexander-Conway et son calcul d’entrelacsIl y a un calcul d’entrelacs du polynôme d’Alexander-Conway : Ñ K( z)qui est facile à établir d’après ce que nous venons de dire :
Il n’a aujourd’hui qu’un rôle historique à jouer, puisque c’est de ce polynôme que les choses ont commencé à bouger dans cette orientation des recherches, le polynôme pour Alexander et le calcul d’entrelacs pour Conway. 4. Les dérivés du polynôme Homfly Le polynôme Homfly est invariant pour les isotopies d’ambiances. a1 - Son polynôme régularisé HK ( a, z) PK ( a, z) = a–v(K) . HK ( a, z) Cette expression le définit, mais il a aussi un calcul d’entrelacs.
Où l’on voit qu’il n’est invariant que pour les isotopies régulières. Il est sensible à la présence ou à l’absence de boucles et correspond aux objets posés sur la sphère soumis aux déformations solidaires de cette sphère M2 et T3, ce qui les différencie des isotopies d’ambiance non solidaires d’aucun support. a2 - Le polynôme rotationnel orienté C’est le dernier polynôme que nous considérons ici parmi les polynômes connus. Il s’obtient grâce à un changement de variable :
Moyennant un polynôme H~K ( a, z) obtenu à partir du précédent par une légère modification :W K ( a, a’, z) = (a’) rot(K) / 2. H~K ( a, z)avec : H~K ( a, z) = [( a–a–1) / z] HK ( a, z)
et où rot(K) est la somme des cycles orientés produits par l’algorithme de Seifert, défini au premier chapitre. Il correspond aux objets orientés posés sur le plan, c’est-à-dire la sphère trouée, et soumis aux déformations solidaires de ce plan M2 et T3.
Ce polynôme peut aussi être calculé à partir de la figure de l’objet par une déclinaison en inversions et lissages de ses croisements, soit le calcul d’entrelacs défini ainsi :
avec r =(a - b-1) / z et l =(b - a-1) / z
et les distinctions suivantes :
L’intérêt de ce dernier polynôme réside dans sa très grande proximité avec la figure qu’il connote et la sensibilité qu’il présente à ce que nous avons thématisé sous le titre de la dualité. Le facteur de dualité qui correspond à un déplacement du trou de la sphère. Il suffit de se reporter aux deux familles de zones déterminées par le premier temps de notre algorithme. Le déplacement du trou de la sphère s’effectue d’une zone appartenant à l’une de ces familles à une zone de l’autre. Ceci est équivalent au changement de plein et de vide dans la dualité, soit le changement du vide qui est autour de la figure d’une famille de zones à l’autre. Nous avons convenu de considérer comme vides les zones de la même famille que celle qui est autour de l’objet considéré. 5. Les polynômes de nos coloriages Nous multiplions chaque polynôme par le facteur mC(K) ou a’C(K) qui nécessite la présence de la surface d’empan, soit la distinction des pleins et des vides, du fait que le nombre de croisement C(K) est orienté par la torsion. L* K (m, n, z) = m C(K) . LK (n, z)ainsi : F* K (m, n, z) =n –v(K) L*K (m, n, z)et : < K >*(A) = L* K (A, –A3, A + A–1)V* K(t) = F*K (t–1/4, –t–3/4, t–1/4 + t1/4)Alors que : P* K (a’, a, z) =a’c(K) PK (a, z)ainsi : P* K (a’, a, z) = a–v(K) . H*K (a’, a, z)et : V* K(t) =P*K(t–1/4, t , t1/2 – t–1/2)Or nous construirons le polynôme rotationnel orienté modifié, un peu différent de ceux de la série qui précède : W* K (m, n, a, a’, z) =m C(K) . n-v(K) . (a’)rot(K)/2 . [( a–a–1) / z] . HK(a’, a, z)6. Les changements de variables Nous recensons les correspondances dont nous avons fait état : Nous pouvons en déduire : A = a –1/4 = a’n = – a–3/4 = – (ab)–3/8Deux remarques 1. En premier lieu, à propos de la conversion de z à z par l’intermédiaire de t. Dans les calculs effectifs, cette remarque intervient : z = t 1/2 – t-1/2 = (t1/4)2 – (t-1/4)2z = (t 1/4 + t-1/4) . (t1/4 – t-1/4) = z . (t1/4 – t-1/4)2. En second lieu, un calcul simple qu’il faut avoir présent à l’esprit : a = (ab) 1/2a’ = (ab -1)1/2a2 = (ab) a = (aa’) a’2 = (ab -1) b = (aa’-1)a = (aa’) b = (aa’-1)Nous avons introduit une nouvelle variable m que nous couplons avec n. Dans les polynômes des cas colorés, nous trouvons d’autres correspondances aux travers des changements de variables successifs : m = Am = t-1/4Donc : m = a -1/4 = a’ = (ab-1)1/2De façon à retrouver, entre m et n avec deux autres variables x et y, le même type de calcul qu’entre a, a’, a et b, nous posons : m = (xy-1)1/2 m2 = (xy-1) x = (mn)n = (xy)1/2 n2 = (xy) y = (m-1n)Maintenant, compte tenu des exposants dont sont pourvus ces variables dans les expressions polynomiales : m c(K)n –v(K)où c(K) est le nombre de croisements orientés par la torsion et v(K) la vrille, soit le nombre de croisements orientés par la caractéristique, nous pouvons suivre l’effet de ce calcul dans l’expression p définie par le produit : p = mc(K) . n–v(K)p = (xy–1)1/2 c(K) . (xy)1/2 (– v(K))p = x1/2 [c(K) – v(K)] . y-1/2 [c(K) – v(K)]Or selon nos définitions correspondant aux figures :
[c(K) – v(K)] = 2 k iS[c(K) + v(K)] = –2 k* iSdonc : p = x kiS . y k*iSoù nous retrouvons les parties coupures et non-coupures de nos schémas plats. Ou encore : p = (mn) kiS . (m–1n) k*iSRevenons aux polynômes où nous allons faire usage de ces calculs. 7. Les calculs d’entrelacs de nos polynômes Parmi les polynômes que nous introduisons avec nos coloriages, certains d’entre eux ont un calcul d’entrelacs.C’est dire qu’ils peuvent être calculés sur la figure ou tout au moins à partir de celle-ci. Ce sont les polynômes suivants. D’abord L* K (m, n, z), puis < K >*(A) et V*K (t) qui s’en déduisent. Ensuite P*K ( a’, a, z) et son régularisé H*K ( a’, a, z) dont peut se déduire également V*K (t). Par contre, le rotationnel orienté modifié W*K (m, n, a, a’, z) nécessite un calcul qui lui est propre.Les autres polynômes nouvellement définis n’ont pas de calcul, ils sont exclusivement déductibles de ceux-ci. 1 - Le polynôme L*K et son calcul d’entrelacsNous commencerons par donner : L* K (m, n, z)Rappelons que nous l’avons défini comme : L* K (m, n, z) = m C(K) . LK (n, z)Il se calcule grâce aux formules suivantes :
Ainsi nous pouvons calculer F* K (m, n, z) grâce à l’expression suivante :F* K (m, n, z) = n–v(K) L*K (m, n, z)et : < K >*(A) = L*K (A, –A3, A + A-1) V* K (t) = F*K ( t1/4, –t-3/4, t-1/4 + t1/4) 2 - Le bracket polynôme modifié< K >*(A) est susceptible d’un calcul grâce aux formules suivantes :
a3 - Le polynôme orienté à 2-variables (Homfly) modifié et son calcul d’entrelacs D’autre part nous pouvons déterminer P* K (a’, a, z) grâce au calcul suivant :
a4 - Son polynôme régularisé et modifié H* K (a, z)Nous pouvons aussi calculer H* K (a’, a, z) par un procédé analogue :
Et V* K (t) s’obtient par le calcul selon les données suivantes :
a6 - Le polynôme rotationnel orienté modifié Et enfin le polynôme rotationnel orienté modifié : W* K (m, n, a, a’, z) = mc(K) . n–v(K) . WK (a, a’, z)
avec : r = (a - b–1) / z, et l = (b - a–1) / z
et les distinctions suivantes :
© 1999 Topologie En Extension . Tous droits de reproduction et de représentation réservés. Tous les textes, dessins et graphiques reproduits dans cet ouvrage sont protégés par des droits de propriété intellectuelle détenus par Topologie En Extension. Par conséquent, aucun de ces éléments ne peut être reproduit, modifié, transmis, rediffusé, traduit, vendu, exploité commercialement ou réutilisé de quelque manière que ce soit sans l'accord préalable écrit de Topologie En Extension. |
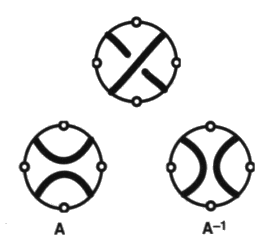 Fig. 1
Fig. 1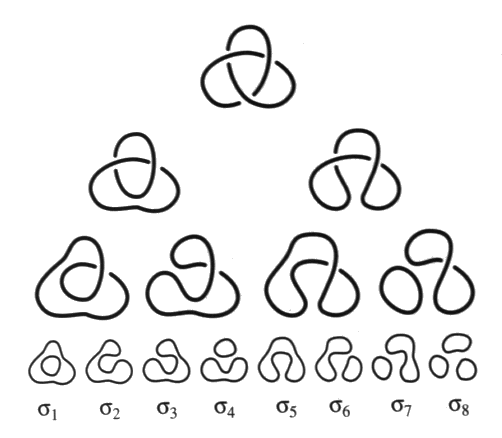 Fig. 3
Fig. 3 >
= A < K
>
= A < K 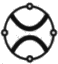 > + A
> + A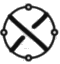 = z ( L
= z ( L –
t-1 V
–
t-1 V = (t1/2
– t-1/2) V
= (t1/2
– t-1/2) V