Chapitre II La méthode de lecture de l’un nœud 1. Analyse d’un exemple de nœud Le titre que j’ai choisi pour ce chapitre indique quelle approche du problème du nœud je suis incliné à suivre, parmi les moins traditionnelles. Je me propose de montrer ce qui du nœud est susceptible d’être lu et si je contribue à éclaircir quelques-unes des questions traitées par la littérature scientifique concernant les nœuds, ce ne sera là qu’un profit accessoire, un à-côté du problème essentiel que j’ai à résoudre. Ma supposition que les nœuds se prêtent à être lus me place ailleurs, entre chiffres, lettres, graphismes et dimensions plastiques, malgré les théories en vigueur, et en fait malgré toutes les théories des nœuds [18 a et b]. Changer de topologie, c’est changer d’objet, comme le dit Quine [57, p. 119] dans un autre contexte. Mais ce n’est pas oublier la théorie classique. Prétendre à une lecture mérite quelques explications. Nous prenons soin de ne pas dire que cette pratique du nœud est une écriture, de ne pas écrire que le nœud est une lettre. Dire cela est un autre problème qui nécessite quelques précisions préliminaires pour que quiconque puisse prétendre assumer les conséquences de la réponse que nous entendons lui donner. Nous ne donnerons pas ici notre théorie de l’écriture. Nous nous restreignons pour l’instant à montrer que ces nœuds et ces chaînes sont lisibles, comme il y a de la lisibilité dans les encoches pratiquées sur l’os retrouvé au Mas-d’Azil et conservé au musée de Saint Germain-en-Laye. Cette phase de lisibilité est nécessitée pour donner lieu à l’écriture comme telle, avant même que nous puissions parler d’une écriture constituée, avant donc que nous puissions prétendre à une écrire spécifique dans la psychanalyse. Renversant ainsi l’ordre naïf de précession entre l’écriture et la lecture [53] et [2 Sém IX, leç du 20.12.61 et du 10.1.62], nous parlerons de la lecture d’objets que nos esprits modernes auraient tort d’assimiler à une projection imaginaire, voire animiste. Ce terme n’explique rien comme il en fut de celui de suggestion à propos de l’hypnose avant la découverte freudienne de la libido. Écrire sera donc une autre étape, le fait de ceux qui, liées entre eux par un discours, un lien social, se servent, dans leur pratique effective, du matériau déjà là, ou d’un autre, mais toujours matériau de récupération, reste d’un autre discours tombé en désuétude. Nous ne voulons d’abord que préciser en quoi notre emploi du terme de lecture n’est pas une analogie, comme c’est souvent le cas. En quoi lire une présentation de tels objets n’est pas lire dans le marc de café. Ici, reste la distinction entre le calcul et la langue où vient se placer la métaphore, dont le principe est la condensation signifiante qui tient à une involution. Or la lecture est une telle involution entre le regard et la voix. La présentation la plus assurée de cette structure est donnée dès notre premier fascicule, en termes de vérité d’abord, pour l’étendre au dire, l’énonciation insoluble aux communicationnistes qui n’en peuvent mais. Le dire nous conduit au nœud [59 c et d]. Comme nous avons pu le constater, les théories scientifiques du nœud ne placent pas au premier chef de leurs préoccupations le problème de la lecture, il est déjà entièrement assumé par le composant algébrique de leur approche. Pour elles, il est moins visible que le nœud soit l’occasion d’un acte à accomplir par le sujet qui pratique l’objet et qui se perd, en une condensation des chiffres qui ruissellent à son propos. Elles visent à une tentative de substituer une écriture connue à un corps topologique et ne distinguent pas les deux étapes, graphique et plastique, après celle de l’observation empirique Ainsi, ces deux aspects, graphique et plastique, sont très peu différenciés à propos de l’identité des nœuds reconnus grâce aux invariants algébriques de la mathématique standard. Celle-ci cherche à remplacer, au titre de la topologie algébrique, l’objet plastique par un groupe algébrique1 ou un polynôme2, cet objet de l’algèbre est un cas particulier dans une vaste famille d’invariants plus sophistiqués et déjà connus [18 c, et 19]. Ceci est un premier point. Dans notre approche, la formalisation de l’objet ne se confond pas avec la mathématisation. À la manière de la formation des énoncés elle se distingue de la démonstration des thèses dans un langage formel en logique mathématique. Cette confusion à pour cause, plus que pour conséquence, l’oubli où se produit notre aliénation signifiante. Notre formalisation, au contraire, tient compte de la condensation puisqu’elle est une formalisation graphique des présentations de ces objets topologiques et une mathématique de leur plastique. Ceci est le point principal, dont des exemples, ici, se trouvent avec le coloriage, la coupure, la dualité des présentations, le graphe de Terrasson, les montages réguliers, les mouvements gordiens et le mouvement nœud. Le chiffrage a une histoire et l’absence de distinction entre le calcul et la langue joue un rôle éminent dans l’inertie qu’il y a à reconnaître les gestes effectifs accomplis dans ces pratiques. Il y a du sujet à cette étape, même s’il est voué à sa destitution dans l’achèvement du processus Puis vient l’étape de la mathématisation, si elle a lieu, lorsque se trouve une structure, dont le prototype reste l’exemple des structures algébriques et leur rôle en théorie des nombres. Il y a là une conversion, au sens psychanalytique du terme, d’une série d’index en symbole du fait de cette structure qui fait texte, comme contexte à ces éléments. Cette lecture suppose que le dessin est l’occasion d’une involution entre le lieu (topos) et le discours (logos) corrélés au regard et à la voix. Nous le considérerons comme accomplissant une coupure, qui est fondée à seulement le faire lituratterrir une fois mise à plat et à écrire, en algèbre, par des petites lettres, les chiffres que nous pouvons lui assigner ou les attribuer à ses singularités et qui ruissellent ainsi à son propos. Cela peut s’effacer dans la pratique mais nous ne pouvons pas l’oublier ni le méconnaître si nous prétendons nous en servir. De fait, il est des théorèmes portant sur le graphisme et la plastique du nœud. Définissons l’involution signifiante qui fait l’objet de notre topologie, comme « la copule qui unit l’identique avec le différent » [2 Sém XIV, leç 15.02.67]. Nous montrerons, du même fait, du côté du chiffre et de l’algèbre, ce qui échappe à cette présentation graphique, le problème des objets non alternables, mais qui se trouve traité par l’aspect plastique enfin isolé. Soit, ce qui s’oublie mais insiste par sa présence plastique, montrant ainsi la difficulté topologique principale de toutes théories futures du nœud. Ayant insisté sur la différence entre la formalisation et la mathématisation, il nous faut souligner, dans l’approche de cette involution, l’existence de « la charte de la structure » soulignée par Lacan [É a’ 21 p. 75] à l’occasion de l’exemple, majeur dans l’histoire, de la formule de la gravitation de Newton. Cette formule ne peut pas se comprendre, mais elle est explicative, éclairante et surtout résolutoire. Lacan introduit ainsi à son propos la notion de la fonction littorale de la lettre, pour désigner son effet de bouleversement rétroactif [É a’ 23 p. 5]. Où l’on peut se saisir qu’aux extrêmes ce n’est pas la trace, ni l’impression, qui soutiennent la métaphore de la lettre qu’il emploie à cette étape et de la pratique de la lecture dans la psychanalyse. Cette pratique est situer comme en mathématique entre celle de l’oracle de Delphe et celle de J.F. Champollion. Pour lier cette question des modes de tenue des énoncés, à ce qui va nous occuper ici, nous retiendrons l’aspect le plus accessible, mais à propos duquel il ne faut pas se contenter, une fois encore, de ressemblances grossières. Dans le registre du matériau, montrons comment les chaînes et les nœuds se proposent comme une pratique couvrant l’ensemble du spectre de l’écriture. Ce spectre va du mathème au poème. Ils se trouvent liés si nous n’oublions pas l’involution signifiante qui est au principe de cette gamme. Dès l’usage d’une simple lettre en logique jusqu’à la pratique de la calligraphie. Aperçu par Wittgenstein celui-ci remonte aussitôt sur le trottoir. Nous apportons par là notre contribution, avec ces quelques précisions aux développements nécessités par les indications données par Lacan. — Il s’agit du côté du mathème pour les chaînes et les nœuds de relever de la tenue d’un énoncé, d’un texte, d’une écriture, comme cela se fait en logique symbolique avec la notion grammaticale des énoncés bien formés mais qui risque, comme nous y avons déjà insisté, de masquer le reflet de la signifiance si on n’y prête garde. Cette tenue peut être poussée très loin en toute rigueur dans leur usage strict comme nous le montre la notion d’assemblages en théorie des ensembles. Ici c’est la tenue qui est masquée usuellement par la signifiance comme en témoignent les rédacteurs des Livres signés N. Bourbaki. Ces assemblages ne désignent pas des ensembles, ils sont ces ensembles même [2 Sém XX, Encore, pp. 46-47]. Nous parlerons à cette occasion de l’usage strict de la lettre en mathématique. Par exemple dans le Livre I de Bourbaki, intitulé Théorie des ensembles [40 p.E II.6] le caractère appelé ensemble vide :
Ce caractère strict est peu aperçu et peu étudié pour une raison qui tient à l’interdit de l’existence de la structure même. Nous pourrions alors revenir sur le lien de l’intuition, pas seulement mathématique mais aussi bien philosophique, à la tenue des énoncés dont l’écriture est encore à venir. La qualité de nœud et, parmi cette dernière, de chaînœud borroméenne, aura cette fonction de tenue à la différence d’autres chaînes, mais ceci ne suffit pas. Il ne faut pas oublier entre énoncé et énonciation, entre langage objet et métalangage que cette tenue tient au sujet mais peut toujours être formalisée jusqu’à la destitution de ce sujet. Il est vrai que cet usage strict s’épuise très vite à se soutenir dans les faits, à la hauteur de l’introduction de certains symboles de fonction. Particulièrement en mathématique classique à l’occasion de l’introduction du mathème (f : a ® b) qui écrit l’application en théorie des ensembles [52, p. 21]. Cet épuisement nécessite d’autres efforts de formalisation mais ne les répudie pas tous. — Du côté du poème, l’écrit va jusqu’à convenir à l’art qui se pratique avec de l’encre et un pinceau, l’écriture poétique chinoise [42]. Il est une fonction de l’écrit, éminemment métaphorique, à condition qu’elle ne doive plus rien à l’analogie ici non plus, dont la référence doctrinale se trouve dans un écrit de J. Lacan (é a 19 pp. 493-528) lorsqu’il traite de l’instance de la lettre dans l’inconscient. Comme nous l’expliquons, dès la présentation de cette série d’ouvrages, cette fonction va jusqu’à l’exemple de l’écriture de leur langue, empruntée à la Chine, par les Japonais, telle qu’elle est mise en pratique, de manière usuelle, dans le discours de l’analyse et en assure un pôle de matérialité. Donnons un nouvel exemple d’une telle écriture, lequel ne vaut seulement que de l’ensemble des résultats réunis dans cet ouvrage.
Nous tenons que le nœud peut s’insérer dans une écriture topologique des trous, lieu d’existence de la structure du sujet, comme un chaînon important, semblable à d’autres et d’égale valeur. Cette écriture de la dérive (drive, Trieb) réalise ce qu’en dit Freud [1 d], ce que précise Lacan [É a 30, pp. 846-850], elle dépend du bord, le nœud, à condition d’y placer une surface, la libido, qui se révèle présenter une structure, le désir, notre coupure. Nous avons commencé à élaborer cette topologie des trous, au travers de la théorie des surfaces intrinsèques3 nous la poursuivons ici. Cette lecture du nœud implique, avons-nous dit, de lui assigner une structure topologique, composant assuré par les différentes théories dont cet ouvrage expose les définitions. Que dirait-on d’un lettré japonais qui prétendrait méconnaître, lors de la lecture d’un texte écrit en japonais, la lecture archaïque chinoise des lettres qu’il emploie pour écrire le japonais contemporain? Nos contemporains peuvent prétendre ne lui accorder qu’une importance de pure érudition, prétendument dépassée, forclose depuis la disparition de Lacan, l’horreur reste toujours liée à l’interdit en acte, en particulier dans la psychose puisque cet interdit revient dans le réel. Nous retrouverons cette pratique de lecture dans notre dernier chapitre afin de donner une présentation nodale de la clinique du sinthome avec les structures freudiennes de la névrose, de la perversion, de la psychose et de l’analyse, et leur articulation mutuelle qui fait tant de difficultés de lecture aux analysants de Freud et de Lacan faute de leur composant topologique construit ici. Il y a là, si nous prenons en compte l’ensemble de ce spectre de variation, l’exercice effectif d’une pulsation entre dimension graphique et aspect plastique de l’objet dont nous avons déjà4 souligné la présence invisible à propos des masques et des tatouages, pour être au principe de l’identification au sens freudien [59 a]. Il s’agit d’autre chose que du recourt à l’image [46] dans l’explication de la fonction des symboles [49, p. 652] [53]. Cette question est à reprendre à partir du personnage gidien comme le souligne Lacan [É a 27] en rendant hommage à J. Delay qui la thématise effectivement au début de son essai sur la jeunesse de Gide, mais cet aspect doit être prolongé jusqu’où nous le menons ici. C’était notre second point. En troisième lieu, en vue de cette pratique des dessins, nous construisons un algorithme qui faisait défaut jusqu’ici et nous l’appliquons jusqu’à en extraire une formule de la gravitation nodale qui lui correspond. Cet algorithme, élargi à plusieurs ronds, est exigé par cette topologie, comme Lacan le soulignait dans une leçon de son séminaire [2 Sém XXI, leç 12.03.74]. Algorithme plus rigoureux, dont il souhaitait la construction alors, pour le nœud en tant qu’il intéresse plus d’un rond de ficelle, comme il s’exprime, et prolongeant, il le dit par la suite, le lemme de Dehn bien connu dans le cas des nœuds propres, faits d’un seul rond. Nous nous proposons, du même geste, d’entreprendre de traiter de l’articulation du un et du multiple [55]. Car il faut ici être attentif au fait que Lacan évoque, en plus de cet algorithme, dans cette même leçon, à un moment précis de son enseignement, un passage qu’il dit avoir déjà effectué du nœud borroméen (plusieurs ronds) au nœud trèfle (un seul rond). Il avait en effet, l’année précédente, dans son séminaire [2 Sém XX, p. 111], juste effleuré l’indication selon laquelle il est nécessaire de se reporter au nœud borroméen afin d’étudier le premier nœud premier, le nœud de trèfle5. Cette remarque va nous occuper encore longtemps, si nous relevons que Lacan a employé ce procédé seulement dans la dernière leçon de séminaire de l’année 1979, au mois de décembre [2 Sém XXVII] avant de dissoudre son École en janvier 1980. Nous ne savons pas qu’il ait jamais explicitement définit ce passage, que nous allons pourtant bien construire, avec le mouvement nœud6, grâce aux moyens que nous voulons donner maintenant. Il est aussi remarquable, et cela mérite d’être noté, que cette leçon du séminaire [2 Sém XX, leç 15.05.73, pp. 111-113] est construite selon le même plan et présente les mêmes objets que le chapitre traitant de nœud dans un ouvrage de divulgation des mathématiques [58, pp. 261-268]. Précisons la terminologie que nous adoptons pour commencer à parler de notre objet. Lorsque nous étudierons un plongement de plusieurs ronds, nous parlerons de chaîne (link). Lorsque nous étudierons un plongement d’un seul cercle, nous parlerons de nœud propre (knot), pour suivre la terminologie de Conway (proper knot) [8]. Cette précision est d’importance ici, car il va se découvrir, du fait de notre analyse, l’existence de chaînes à coupures constantes. Nous appellerons nœuds impropres ce type de chaînes ou encore chaînœuds (linknots). Dans tous les cas, nous parlons d’objets lorsqu’il s’agit indifféremment de chaînes ou de nœuds. Nous commencerons par formuler, dans ce chapitre, l’algorithme pronostiqué par Lacan. Nous travaillons à partir des présentations (diagrams) de nœuds ou de chaînes mis à plat en position générale7 que nous dirons schémas plats S.
Fig. 1 Dans le cas général, une présentation est non alternée. Nous dirons qu’une présentation est alternée si, à parcourir successivement chaque composant, chacun des brins de ficelle passe alternativement au-dessus lorsqu’il est passé en dessous et au-dessous lorsqu’il est passé au-dessus des éléments de ronds de ficelle qu’il rencontre successivement.
Fig. 2 Nous parlerons d’une présentation non alternée dans le cas contraire. Pour un objet quelconque dans une présentation donnée, si elle n’est pas alternée elle-même, nous ne sommes pas assurés qu’il existe une présentation alternée. Il y a donc des objets alternables et des objets non alternables. À partir du schéma plat S, il peut être tentant, afin de chiffrer l’alternance, de marquer naïvement d’un signe plus (+) les croisements où un composant passe au-dessus et moins (–) les croisements où il passe au-dessous des éléments de ficelle qu’il rencontre.
Fig. 3 Mais l’ironie de cette structure reste qu’à effectuer ce chiffrage sur tous les composants de l’objet, et c’est chose faite dès le premier dans le cas d’un nœud propre, nous constatons que tous les croisements se trouvent marqués de la même manière par la présence à la hauteur de chacun d’eux des deux signes, + et –.
Fig. 4 Proposons un chiffrage de l’alternance qui montre la cohérence de cette particularité et permettra de préciser par la suite, grâce à notre méthode, à quoi tient cette distinction. Chiffrage freudien Nous procédons donc autrement, et même pouvons-nous dire de façon contraire à cette première tendance intuitive. Ici se découvre un chiffrage particulièrement freudien, au sens où il faut que, celui qui a découvert l’Ics, ait été Freud, pour calculer intuitivement comme cela — rappelez-vous de l’interprétation qu’il donne au rêve de “la belle bouchère spirituelle” qui contredisait sa théorie du rêve. Nous ne cherchons même pas à savoir comment ça lui est venu, il nous suffit de le lui reconnaître afin de situer ce dont la psychanalyse dépend. Le désir du psychanalyste comporte cette inconnue. À partir du schéma plat S, nous proposons, afin de chiffrer l’alternance, de marquer un premier croisement d’un signe indifférent, par exemple le signe plus (+). Puis à parcourir chaque composant, à partir des croisements déjà marqués : — de placer le même signe que celui qui précède, à la hauteur du croisement suivant, si ce composant passe de manière alternée d’un croisement à l’autre, — d’inscrire le signe contraire de celui qui précède, à la hauteur du croisement suivant, si ce composant passe de manière non alternée d’un croisement à l’autre.
Fig. 5 C’est dire que nous appliquons un principe de chiffrage que nous formulons ainsi : Lorsque les éléments de corde sont alternés, nous n’alternons pas les signes; lorsque les éléments de corde ne sont pas alternés, nous alternons les signes. Comme cela se voit encore mieux dans le fragment suivant.
Fig. 6 Nous qualifions de freudien ce type de chiffrage. Effectuons ce chiffrage sur le même exemple, en commençant ainsi :
Fig. 7 Il donne, une fois achevé, le résultat suivant :
Fig.8 où peut se lire qu’il y a, parmi les croisements, deux moitiés alternées en elles-mêmes, mais pas nécessairement connexes, ou si l’on préfère deux sortes de croisements, les croisements marqués plus (+) et les croisements moins (–). Nous introduirons une nouvelle orientation8 dans le champ de ces présentations afin de rendre compte de ce fait, afin de donner un sens à ce chiffrage qui pour l’instant n’existe que par sa pertinence graphique.
Fig. 9 Donnons, en trois dessins, les étapes principales de l’analyse que nous allons mener par des coloriages grâce à notre algorithme, à propos de chaque nœud, à propos de chaque chaîne.
Fig. 10 Les couleurs que nous adoptons sont ici rendues par des trames utilisées de manière immuable. Leur fonction respective apparaîtra au cours des différents temps. 2. Les trois temps algorithmiques Nous présentons maintenant un premier coloriage très simple à effectuer dans l’étude de chaque nœud ou chaîne mis à plat. 2.1. Premier temps : la surface d’empan Il définit la surface d’empan de la présentation donnée.
Fig. 11 Il vise à révéler une surface dans le dessin de l’objet mis à plat; il s’agit d’une surface vraie dessinée sans ses plis. Les plis paraissent sous l’aspect de demi-torsions de bretelles. Nous obtenons un damage du plan. Munis d’un binaire de signes, nous parcourons et marquons l’ensemble des zones en passant par une traversée franche des portions d’arc10 et en changeant de signe de l’une à l’autre. Cette traversée se fait en plein milieu de chaque portion d’arc, en évitant les croisements et leur proximité. Toutes les zones adjacentes de la mise à plat sont alors marquées de signes contraires, sachant que deux zones adjacentes sont séparées par une portion d’arc.
Fig. 12 Pour définir la surface d’empan sur l’exemple de notre objet, donnons nous un couple de signes, comme (+, –) ou (0, 1), ou (blanc, gris) ou tout autre couple de signes distincts et opposés qu’on utilise comme éléments différentiels premiers. Commençons par placer l’un des signes dans une zone quelconque en utilisant ici le binaire (0, 1).
Fig. 13 Le signe 0 est écrit dans une première zone. Passons franchement, en plein travers d’une portion d’arc, dans une zone adjacente. Nous écrirons 1 dans la zone atteinte. Puis à partir de cette zone marquée 1, passons dans une autre en traversant une autre portion d’arc où nous écrivons 0. Poursuivons ainsi de zone en zone en traversant toujours de la même manière les portions d’arc, en évitant les croisements, jusqu’à ce que toutes les zones portent un signe (0 ou 1).
Fig. 14 Remarquons que cet algorithme n’aboutit jamais à une situation contradictoire : une même zone ne portera jamais deux signes contraires; de part et d’autre d’une portion d’arc il n’y aura jamais le même signe, comme le confirme le théorème de Jordan de la théorie des courbes planes. Nous obtenons donc deux ensembles distincts de zones : celles qui portent le signe 0 et celles qui portent le signe 1.
Fig. 15 Fin du procédé algorithmique. Nous adoptons alors un principe terminologique qui va nous permettre de définir la surface d’empan d’une présentation. La surface d’empan d’une présentation Nous convenons de ce qui suit. L’ensemble des zones qui portent le signe de la zone périphérique est l’ensemble des vides de la présentation donnée. De ce fait, nous définissons l’ensemble des pleins de cette présentation par l’ensemble des zones portant le signe opposé à celui de la zone périphérique. Ainsi l’ensemble des pleins, respectant cette convention, connectés par les demi-torsions, définit la surface d’empan de la présentation. Colorions cette surface pour la mettre en évidence, le nœud ou la chaîne se présente alors comme un damier déformé.
La surface d’empan de la présentation donnée. Fig. 16 Nous notons P le nombre de zones pleines (ici, P = 11) et V le nombre de zones vides (V = 10), en n’oubliant pas la zone extérieure. Le premier temps de l’algorithme est terminé. Or, si nous notons C le nombre de croisements, nous disposons de la formule déduite de l’indicateur d’Euler-Poincaré11 de la sphère, à l’occasion du pavage de cette sphère par le graphe des pleins, ou son dual, le graphe des vides12. Cette formule nous dit que le nombre de pleins (sommets du graphe des pleins) diminué du nombre de croisements (arêtes du graphe des pleins) augmenté du nombre des vides (faces du graphe des pleins) est toujours égal à deux sur la sphère. Ceci s’écrit : P – C + V = 2 que nous pouvons transformer grâce à un petit calcul fait à la ressemblance du calcul arithmétique, ce qui est légitime puisque ces lettres sont censées se référer à des nombres. Ainsi : P + V = C + 2 qui nous donne ce que nous appellerons la formule élémentaire du nœud : C = P + V – 2 soit dans notre cas général : C = 11 + 10 – 2 = 19. a4 - Le cas des présentations alternées Dans les cas alternables, dans leur présentation alternée, le nombre minimum de croisements permet la recherche de la présentation de la surface d’empan minimale. Nous désignons, dans ces cas, comme pleins de la surface d’empan minimale l’ensemble des zones les plus nombreuses et comme vides l’ensemble des zones moins nombreuses. Nombre de croisements minimum Nous sommes assurés qu’il existe pour chaque objet des présentations comptant un nombre minimum de croisements; nous les appellerons présentations minimums, mais nous ne savons pas les trouver dans tous les cas. Lorsqu’un objet est alternable, sa présentation alternée est minimum et L. Kauffman a démontré, grâce à son polynôme, dans le contexte du premier temps de notre algorithme qui détermine la surface d’empan, que ce nombre minimum de croisements est un invariant topologique des nœuds alternables. Dans le cas où la présentation alternée est trouvée, nous sommes assurés que l’objet étudié est alternable et par conséquent dans sa présentation minimum. Dans leur présentation alternée, si elle existe, grâce aux coloriages produits par l’algorithme, nous pourrons déterminer le type graphique des objets, cette typologie ne sera qu’une commodité terminologique de départ, au regard de la structure nodale et plastique qui se découvre à partir de là. Ces coloriages restent aussi réalisables dans une présentation quelconque non alternée, et nous fournissent des indications précieuses pour compter les enlacements par exemple ou pour l’emploi des transformations. La surface d’empan minimale Dans la présentation alternée d’un objet alternable, l’ensemble des zones les plus nombreuses, choisies comme pleines, connectées par les demi-torsions, définit la surface d’empan minimale. Les zones vides doivent être les zones les moins nombreuses.
Fig. 17 Ici, la surface d’empan de cette présentation est la surface minimum, car V = 4 est plus petit que P = 5. Mais la surface minimale, définie alors par les pleins, ne correspond pas toujours à la surface d’empan de la présentation donnée telle que nous l’avons définie.
Fig. 18 Par exemple ici la surface de cette présentation n’est pas la surface minimum demandée, car P = 3 et V = 4. Il y a là la nécessité d’un échange de la qualité de plein et de la qualité de vide, d’entre les deux ensembles de zones définis par l’algorithme, afin d’inverser ce rapport et d’obtenir P = 4 et V = 3. Mais la surface obtenue n’est plus la surface d’empan de la présentation donnée, elle ne respecte plus la condition que nous avons imposée à cette surface dans sa définition pour être dite telle. Il s’agit alors de la surface d’empan qui respecte cette définition pour être celle de la présentation duale. Expliquons cela en donnant des définitions précises. La dualité Nous nommerons dualité l’échange des pleins et des vides13 dans une présentation donnée. Surface duale Nous parlerons de surfaces duales entre elles, les deux surfaces obtenues l’une de l’autre par la dualité. Dans le cas envisagé, celui où nous recherchons la surface d’empan minimale d’une présentation alternée, en présence de cette surface minimale, duale de la surface de la présentation donnée, nous devons rester attentif aux définitions. Or la convention précédente, qui définit la surface d’empan d’une présentation, nous oblige à changer de présentation, si nous voulons que cette surface duale soit la surface d’empan d’une présentation, afin que les zones vides soient de même signe que la zone périphérique comme le veut cette définition. Nous passons ainsi à la présentation duale. Présentation duale Il suffit de retourner un arc périphérique, de lui faire parcourir un tour de l’autre coté de la figure pour obtenir la présentation duale d’une présentation donnée. Ou encore, il suffit d’entourer la figure d’un cercle puis de raccorder ce cercle à un arc périphérique. Cet artifice planaire qui consiste à employer un cercle supplémentaire est en fait un changement de présentation. Il s’agit bien de la déformation continue de l’arc périphérique considéré. Montrons ce procédé sur l’exemple que nous avons choisi de prendre depuis le début.
Fig. 19 Ce changement de présentation qui met à contribution tous les croisements de la présentation si nous faisons passer l’arc ainsi déformé au-dessus ou au-dessous de la figure14, est encore plus régulier sur la sphère non trouée car dans ce cas, l’arc déformé parcourt la face cachée de la sphère et ne met à contribution aucun croisement. Ce changement de présentation peut être répété plusieurs fois. Sur la sphère trouée, notre feuille de papier, nous parlerons alors de présentations duales les unes des autres, selon que la zone périphérique, zone portant le trou de la sphère lorsqu’elle est trouée, fait parti de l’une ou de l’autre moitié de zones déterminées par notre premier procédé algorithmique. Nous résolvons ainsi le problème posé par Listing, à la fin de sa thèse d’habilitation, lorsqu’il traite des différentes présentations d’un même objet mis à plat. Il avait repéré ce binaire des zones qu’il avait notées l et q. Nous consacrerons, plus loin, une étude, plus développée, à cette notion très importante dans nos dessins. Ces définitions étant précisées ici, reprenons l’exemple du cas alterné dont nous cherchons la surface d’empan minimale et montrons en quoi elle est la surface d’empan de la présentation duale de celle dont nous disposions en passant d’une présentation à l’autre grâce au procédé, artificiel en apparence, du cercle périphérique supplémentaire, mais que nous prendrons comme définition pratique et graphique de la dualité des présentations.
Fig. 20 La recherche de la surface d’empan minimale dans les cas alternables lorsqu’ils sont dans leur présentation alternée, nous a conduit à changer de présentation par ce mouvement encore énigmatique, la dualité des présentations, qui sera éclairé plus loin. Nous obtenons bien, avec la surface d’empan de cette présentation, la surface d’empan minimum, V < P, de cet objet :
Fig. 21 puisque V = 3 et P = 4 dans ce cas. Il s’agit bien du même objet comme le changement de présentation le prouve. Nous rencontrons aussi le cas de présentations équilibrées. Présentations équilibrées Nous dirons qu’une présentation est équilibrée lorsque P = V. Dans de tels cas, les deux surfaces d’empan duales l’une de l’autre peuvent être indifféremment dite minimales. Les lecteurs de Freud peuvent se souvenir de ce que dit le petit Hans à propos de la girafe chiffonnée. Comme le fait remarquer Lacan [2 Sém IV], si la grande girafe représente la mère, il est plus facile de s’asseoir sur une petite girafe dessinée sur une feuille, marquant ainsi un trait principal de cette observation, puisqu’il s’agit alors d’autre chose que de la vraie girafe. Il y va du symbolique, qui indique le registre en question des bêtises pour le petit garçon à ce moment. Freud y insiste, à un moment de son commentaire, lorsqu’il affirme que Hans n’est pas encore entré dans l’analyse tant qu’il n’a pas mis au point le registre de fictions dont relèvent ses bêtises en question. Cette dimension de fiction, dimension de la vérité que nous avons jugée nécessaire à fonder dans un calcul, c’est l’objet du premier volume, consacré à la logique15, de cette série d’ouvrages d’introduction et de recension de la topologie et des mathématiques du champ freudien. Si nous revenons alors au commencement de cette discipline, la signifiance des rêves, nous pouvons souligner en quoi l’appareil optique évoqué par Freud, lui est nécessaire pour détacher son lecteur du préjugé, toujours aussi tenace aujourd’hui, selon lequel le sujet doit être localisé dans la structure mentale. Lacan est reparti de là, avec son schéma optique un peu plus élaboré. Mais d’où peut suivre l’analyse d’un tableau, et pas des moindres, puisqu’il s’agit des Ménines de Vélasquez, à faire jouer les lignes de construction réelles de la perspective linéaire. Elles ne sont pas localisées dans l’espace, si elles sont reproductibles à tout moment. Il suffit alors de passer aux objets virtuels de notre topologie dont aucun matériau ne donne qu’un aperçu local, pour se saisir du lieu de la structure. Or les animations électroniques peuvent aujourd’hui réaliser l’espace nodal en ce qu’il a de calculable par des processus récursifs; il reste à les lire; pour cela il faut un lecteur. Dans la volonté de Freud de rendre raison de la rhétorique du rêve et de son lieu, celui-ci s’achemine vers la nécessité de cette topologie. Nous ne dirons pas, en une grossière approximation, que le rêve est écrit sur une feuille de papier chiffonnée, parce qu’il est comme noué par le travail du rêve, le désir, il est écrit sur une substance libidinale, dont le texte nous livre l’étoffe. 2.2. Deuxième temps : caractère orientable Il détermine le caractère orientable ou non orientable de la surface d’empan.
Fig. 22 Nous cherchons à décider si la surface produite par le temps précédent est unilatère ou bilatère16. Rappelons les définitions du caractère d’une surface topologique, lorsqu’elle est prise sous son aspect orientable (bilatère) ou non orientable (unilatère). Bilatère : signifie que la surface a deux faces (comme un disque), elle est orientable. Unilatère : signifie que la surface n’a qu’une face (comme une bande de Mœbius), elle est non-orientable. Un principe résulte du deuxième temps algorithmique qui détermine le caractère de la surface d’empan. Il va nous servir à décider de la réponse ou à vérifier le résultat obtenu après emploi de l’algorithme. a2 - Principe résultant du deuxième temps S’il existe au moins un vide de valence impaire, la surface est unilatère. Dans le cas contraire la surface est bilatère, tous les vides sont de valence paire. Définition de la valence des zones Chaque zone est bordée par un certain nombre de croisements; ce nombre définit la valence de la zone. Nous appellerons boucles les zones de valence un, mailles les zones de valence deux et triskels les zones de valence trois. Remarquons que la valence d’une zone donne aussi bien le nombre de portions d’arcs adjacentes à cette zone. L’emploi de ce principe est immédiat. Si tous les vides sont de valence paire, la surface est bilatère. Nous la colorions avec deux trames contrastées, une pour chaque face.
Fig. 23 Dans le cas contraire, il existe au moins un vide de valence impaire, la surface est unilatère. Nous la colorions par des hachures.
Fig. 24 La parité de la valence des zones vides constitue le trait pertinent qui est retenu par ce principe dans la détermination du caractère orientable ou non de la surface d’empan. Avant d’en déduire ce principe, formulons le deuxième temps de notre algorithme. À cette fin, nous parcourons les zones pleines en les marquant de signes distincts. Elles sont connectées entre elles par des demi-torsions. Nous passons cette fois d’une zone pleine à une autre zone pleine en empruntant les demi-torsions. Pour déterminer le caractère bilatère ou unilatère de la surface d’empan, il faut se munir d’un nouveau binaire; prenons (+, – ). Nous marquons au moyen de ce nouveau binaire les zones pleines, en quoi consiste la surface d’empan. Commençons par écrire + dans un premier plein :
Fig. 25 Passons une demi-torsion : écrivons – dans ce second plein. De là, passons par une autre demi-torsion et écrivons + dans cette nouvelle zone pleine,
Fig. 26 Et ainsi de suite en cherchant à emprunter toutes les demi-torsions. — Soit que nous trouvions deux signes opposés dans une même zone.
Fig. 27 Il arrive en effet que nous soyons contraints d’emprunter plusieurs fois une même zone pleine, y étant conduits par des demi-torsions différentes, par conséquent une même zone pleine pourra porter plusieurs signes. De surcroît ces signes ne sont pas toujours identiques entre eux dans une même zone, ils sont alors opposés, auquel cas le procédé peut être interrompu. — Soit que nous ayons emprunté au moins une fois toutes les demi-torsions et que nous ne trouvions aucun couple de signes opposés dans une même zone. Fin du procédé algorithmique. Deux cas peuvent alors se présenter. Premier cas Il n’y a pas de contrariété. Chaque zone pleine ne porte que des signes identiques. C’est le cas de l’exemple suivant.
. Fig. 28 Dans ce cas, de part et d’autre de chaque demi-torsion, les pleins sont de signes différents. La surface d’empan est bilatère, il y a une face + et une face –. Nous dirons que l’objet considéré se présente comme un non-nœud. Deuxième cas Il y a contrariété. Le parcours effectué conduit à écrire + et – dans une même zone pleine. C’est le cas de l’exemple que nous avons choisi :
Fig. 29 Dans ce cas, tous les pleins sont à la fois + et –. La surface d’empan est unilatère, il n’y a qu’une seule face. L’objet considéré se présente comme un nœud. Définition d’une présentation comme un non-nœud L’objet considéré se présente comme un non-nœud, ou encore sa présentation est une présentation en non-nœud lorsque la surface d’empan est bilatère. Comme nous l’avons précisé plus haut, ce caractère n’est pas déterminé avec certitude avant que nous soyons passés par toutes les demi-torsions. Nous sommes assurés qu’une surface est bilatère à cette seule condition. Les présentations non-nœuds ont une surface d’empan bilatère ; nous la colorions avec deux trames contrastées, une pour chaque face.
Fig. 30 Définition d’une présentation comme un nœud L’objet considéré se présente comme un nœud, ou encore sa présentation est une présentation en nœud lorsque la surface d’empan est unilatère. Il se peut que le caractère non orientable de la surface, révélé par cette contrariété des signes en une même zone, n’apparaisse pas aussi vite que dans notre exemple. Tant que les signes marqués dans des mêmes zones sont homogènes entre eux, nous ne pouvons décider avec certitude du caractère de la surface qu’après avoir emprunté toutes les demi-torsions. Les objets, lorsqu’ils se présentent comme un nœud, ont une surface d’empan unilatère; nous la colorions par des hachures.
Fig. 31 Dans le cas où la surface est unilatère, nous pourrons la réorienter, la rendre bilatère. Il est nécessaire et il suffit d’y effectuer une coupure. Cette coupure peut toujours être rendue connexe et se présenter comme un cercle. Ceci sera l’objet de notre troisième temps. Le deuxième temps est terminé. a5 - Monstration du principe déduit du deuxième temps De ce deuxième temps de l’algorithme nous déduisons le principe plus direct que nous avons formulé afin de déterminer le caractère bilatère ou unilatère d’une surface d’empan, et par là, dans les cas alternés, le type nœud ou non-nœud de la présentation considérée. Rappelons le principe que nous voulons déduire maintenant. S’il existe un vide de valence impaire, la surface est unilatère. Nous avons défini la valence des zones comme étant le nombre des croisements ou le nombre des portions d’arcs adjacents à cette zone. À considérer les zones vides uniquement, nous nous préoccupons de la parité de leur valence comme dans notre exemple.
Fig. 32 En effet, la parité de ces nombres a une conséquence immédiate de notre procédé, si nous remarquons qu’il suffit d’effectuer de plein en plein un parcours circulaire autour d’un vide de valence impaire, en écrivant alternativement + ou – à chaque passage de demi-torsion jusqu’à revenir à la zone de départ.
Fig. 33 Le dernier signe et le premier signe, écrits dans la même zone terminale et initiale du cycle, sont différents puisque le parcours décrit un nombre impair de passage par les demi-torsions. Il y a par conséquent contrariété des signes à la hauteur d’une zone. Nous concluons donc que la surface d’empan est unilatère, s’il existe au moins un vide de valence impaire. C’est le principe que nous avons énoncé. Dans le cas contraire, s’il n’y a que des vides de valence paire, ce fait ne se produit jamais, la surface est bilatère. Ce deuxième temps de l’algorithme détermine le principal caractère de la classification des surfaces présentée dans notre ouvrage traitant des surfaces topologiques intrinsèques17. a6 - Le cas des présentations alternées Dans le cas d’une présentation alternée, d’un objet alternable, les deux cas peuvent se présenter. Si sa surface d’empan minimum18 le présente comme un non-nœud, nous dirons que c’est un non-nœud, en tant que les non-nœuds proposent la présentation la plus pure des répartitions des nombres d’enlacements19. Si sa surface d’empan minimum le présente comme un nœud, nous dirons que c’est un nœud au sens où il contient du nœud dans le nouage que caractérise cette présentation. Ce nœud sera révélé par la coupure nécessaire à la réorientation de la surface. Notre propos, par la suite, va consister à calculer le nombre caractéristique de ce nouage et le nombre de nœud qu’il contient. Présentations équilibrées Si la présentation est équilibrée20, c’est-à-dire où P = V, on doit considérer les deux surfaces d’empan minimum. Si l’une des surfaces est bilatère, on le classe parmi les non-nœuds et nous pouvons parler alors de sa surface d’empan minimale. Si les deux surfaces sont bilatères, on le classe parmi les non-nœuds, et les deux surfaces d’empan duales l’une de l’autre peuvent être indifféremment dites minimales. Si les deux surfaces sont unilatères, nous verrons par la suite qu’elles sont caractérisées de la même manière par la coupure. Nœuds et non-nœuds Ainsi dans l’ensemble des nœuds et des chaînes, qui consistent en des enchevêtrements d’un ou de plusieurs ronds de ficelles, nous distinguons, parmi les cas alternables, les nœuds et les non-nœuds comme deux types d’objets plus proches de la vérité du nœud dans sa distinction d’avec l’enlacement. Dans une chaîne, c’est dire ici un enlacement, un des ronds emprunte le trou d’un autre rond. Dans un nœud aucun rond n’emprunte le trou d’un autre rond, lorsqu’un rond rentre dans le trou d’un autre rond, il en ressort [2 Sém XXII, leç du 13.05.75]. Cette distinction est principale dans le premier temps de notre propos, elle est la plus lisible et se trouve fondée par nos coloriages et le commentaire qui les accompagne. Dans ce qui va suivre, au cours des deux chapitres suivants, nous voulons montrer à quel titre le lien, à la fois de l’enlacement et des non-nœuds à surface bicolore, d’autre part du nœud et des surfaces monochromes, est fondé au travers des présentations alternées. Le plus petit non-nœud est une chaîne, c’est un enlacement.
Fig. 34 Il existe des non-nœuds faits d’un seul rond. Ce sont des non-nœuds propres. Le plus petit exemple connu est le nœud que Jacques Lacan propose d’appeler “nœud de Lacan” [2 Sém XXIII, leç du 17.02.76].
Fig. 35 Constatons que les caractéristiques de surface de l’étoffe dépendent de l’enlacement et du nouage du bord, convenant ainsi à la structure de la pulsion (drive, trieb) décrite par Freud, où la constance de la poussée (invariance du groupe fondamental21) est raccordée à la source par l’intermédiaire de son bord (prévalence des orifices corporels, érogénisation par le langage). Il a été nécessaire d’introduire cette surface (quotient du groupe fondamental22), identifiée à la libido comme l’explique Lacan [É a 30, p. 846], pour montrer ce lien crucial dans la structure de la pulsion freudienne. Le nouage et l’enlacement s’effacent comme le chiffonnage de l’étoffe, dans le passage à l’intrinsèque, laissant une trace, sous l’aspect de ces caractéristiques, de ce qu’il y a eu du nœud et de la chaîne. La coupure, que nous introduisons maintenant dans les cas des étoffes monochromes, surfaces non orientables chiffonnées, trace le trajet qui révèle la structure de la libido. Ainsi le lecteur peut se saisir de la remarque de Lacan [2 Sém XIII] selon laquelle ces surfaces non orientables, associées au regard et à la voix, sont nécessaires afin de situer correctement le désir [É a 21, p. 601]. En effet les cas orientables, comme la sphère et le tore, sont insuffisants pour rendre compte de cette articulation, Lacan les associe aux objets des pulsions prégénitales, orales et anales. Nous identifions cette coupure, qui condense la désorientation de la surface, au désir, comme une métonymie [É a’ 21, p. 70]. Ceci est à lire à un moment précis du commentaire de J. Lacan, dans l’involution qu’il pratique entre métonymie et métaphore. Au moment où il commente les explications de Freud, relatives à la double inscription, dans la tentative qu’il entreprend alors, en 1915, d’écrire sa métapsychologie [1 e]. L’interprétation du rêve consiste dès lors à déterminer la coupure, grâce aux matériaux associatifs, soit la caractéristique intrinsèque principale de cette fiction de surface introuvable; Freud l’appelle libido, ce qu’est la substance jouissance qu’il n’y a pas. Cette approche va se révéler plus rigoureuse, sinon exacte, avec le nombre et l’invariance des coupures, lorsqu’elles sont plusieurs du fait du nombre de ronds. 2.3. Troisième temps : la coupure Il détermine le trajet d’une coupure qui réoriente la surface d’empan.
Fig. 36 Dans le cas où la surface est unilatère, nous pourrons la réorienter, la rendre bilatère. Il est nécessaire et il suffit d’y effectuer une coupure23. Cette coupure peut toujours se présenter comme un cercle, si elle présente plusieurs composants, ils peuvent êtres rendus connexes. Pour déterminer la coupure il faut se munir d’un nouveau binaire de couleurs. Prenons deux trames contrastées gris clair et gris foncé :
Colorions en alternance au moyen de ce binaire de couleurs, les portions d’arcs de chaque rond en suivant les parcours successifs de ces ronds et en déposant de la couleur du côté de la surface non orientable produite aux deux premiers temps comme dans notre exemple que nous reproduisons ici.
Fig. 37 Nous commençons par colorer une portion d’arc, avec une des deux couleurs prise indifféremment.
Fig. 38 Il faut constater, afin de rester du coté de la surface d’empan, que celle-ci oblige à changer de côté à la hauteur de chaque croisement. C’est à cet endroit que l’on change de portion d’arc et par conséquent de couleur.
Fig. 39 Nous poursuivons ce coloriage jusqu’à ce que chaque portion d’arc ait une couleur pour le rond que nous sommes amenés à longer de cette manière.
Fig. 40 Lorsqu’il s’agit d’un nœud propre, d’un seul rond, la détermination de la coupure est terminée à la fin du parcours. Quand il s’agit d’une chaîne, la procédure de coloriage des portions d’arcs d’un même rond revient sur son point de départ sans avoir coloré l’ensemble de la surface. Il nous faut recommencer autant de fois qu’il est nécessaire en fonction du nombre de ronds, en choisissant de commencer par une portion d’arc quelconque et une des deux couleurs, ceci pour chaque rond. Différence entre un et plusieurs ronds Lorsqu’il s’agit d’une chaîne, l’algorithme connaît un premier temps d’arrêt, il se bloque. La procédure de coloriage des portions d’arcs d’un même rond revient sur son point de départ sans avoir coloré l’ensemble de la surface. Il nous faut recommencer cette période, en choisissant de commencer par une portion d’arc quelconque et une des deux couleurs :
Fig. 41 La procédure se poursuit le long de la seconde composante jusqu’à la parcourir dans son ensemble.
Fig. 42 La procédure s’interrompt de nouveau, alors nous passons une nouvelle fois à un autre rond en adoptant arbitrairement une nouvelle portion d’arc et une des deux couleurs.
Fig. 43 Nous poursuivons ainsi jusqu’à longer le dernier rond.
Fig. 44 La procédure de coloriage est ainsi terminée. Fin du procédé algorithmique. Il nous reste à l’interpréter par le dessin de la coupure. À partir de ce coloriage, certains pleins sont monochromes, car toutes leurs portions d’arcs sont de la même couleur, d’autres sont bicolores.
Fig. 45 Il y a deux sortes de zones. Les pleins monochromes peuvent être coloriés de la couleur des portions d’arcs qui les bordent. Les pleins bicolores sont tenus par des croisements où se rencontrent, dans la même zone pleine, deux portions d’arcs de couleurs différentes. Nous appellerons ces croisements, des croisements coupures.
Fig. 46 Nous pouvons esquisser la coupure en séparant les deux couleurs à la hauteur de chacun de ces croisements par un fragment de bord qui consiste dans les zones pleines. Et c’est à réunir ces fragments de bords qui consistent que nous obtenons les composants de la coupure. La coupure passe par chacun des pleins bicolores de manière à séparer les deux couleurs. De fait cela équivaut à dire que la coupure passera autour du ou des vides dont toutes les portions d’arcs sont de même couleur.
Fig. 47 La coupure, en parcourant les pleins bicolores, joint les croisements coupures. Le troisième temps est terminé. Coloriages et orientations Ce coloriage défiinitif correspond de manière stricte à une orientation des ronds de chaîne et de nœud24, selon le principe de correspondance suivant.
Un sens d’orientation d’un élément de ficelle est donné par une couleur déposée d’un côté de cet élément de corde. Pourvu de cette correspondance choisie, une orientation des ronds qui font bord de l’étoffe peut être associée à un coloriage de l’étoffe.
Fig. 48 Une autre manière de noter le code adopté peut être étendu usuellement au plan des dessins, les zones colorées d’une couleur donnée voient leur bordure orientée d’une manière correspondante.
Partie nœud et partie non-nœud d’une présentation Dans une présentation colorée donnée, nous parlerons de la partie nœud (partie coupure) pour le composé des zones pleines traversées par la coupure et des croisements par où passe la coupure. Cette partie peut présenter plusieurs composants. Nous parlerons de la partie non-nœud (partie non-coupure) pour le composé des pleins monochromes et des croisements par où ne passe pas la coupure. Elle peut aussi présenter plusieurs composants. Ces parties sont isolées sur les dessins à suivre le tracé d’un sous-graphe du graphe de Terrasson25 :
Fig. 49 Les sources d’où proviennent ces différentes parties26 et leur mode de composition27 font l’objet d’études spécifiques. Avec la définition de la partie nœud et de la partie non-nœud d’une présentation colorée, l’algorithme est terminé. a4 - Le cas des chaînes faites de plusieurs ronds Dans le cas d’une chaîne faite de plusieurs ronds, nous avons vu que la procédure s’interrompt et qu’il nous faut la reprendre de manière arbitraire en choisissant une nouvelle portion d’arc et une couleur. Un choix différent peut être effectué, parmi les deux couleurs, pour la portion d’arc choisie à ce moment de la reprise du coloriage. Ces différents coloriages ne produisent pas le même résultat : il y a donc plusieurs coupures possibles dans le cas d’une chaîne à plusieurs ronds. En voici un exemple à partir du cas général :
Fig. 50 Dans le cas des chaînes, il y a donc plusieurs coupures. Si le nombre de ronds est noté r, le nombre de coloriage est (2r) et le nombre de coupures est (2r–1). Ces différentes coupures ont la même parité. La théorie des surfaces topologiques intrinsèques28 nous assure de ce fait puisqu’il s’agit toujours de la même surface non orientable et qu’elle est équivalente à un plan projectif (cas impaires) ou à une bouteille de Klein (cas pairs) à laquelle est adjoint un certain nombre de tores d’après le théorème principal de la théorie des surfaces intrinsèques. a5 - Les quatre interprétations du rêve de “la belle bouchère” Lacan donne un exemple d’interprétation de rêve [É a 21, pp. 620 à 627], il dit qu’il ne le fait pas souvent mais qu’en l’occasion il l’a porté au paradigme. C’est le rêve de “la belle bouchère spirituelle” transcrit par Freud dans son ouvrage majeur [1 a]. La première interprétation de Freud est déjà assez surprenante quand on sait qu’il s’agit d’un rêve que cette dame apporte au psychanalyste en contradiction à sa théorie des rêves selon laquelle un rêve est l’accomplissement d’un désir. Freud le présente bien ainsi et il faut qu’il soit Freud pour répondre à la belle hystérique qu’elle a le désir d’avoir un désir insatisfait. Puis il complète son commentaire par les premières lignes qu’il donne de la théorie de l’identification, spécialement hystérique, ajoutant ainsi une deuxième interprétation, dont il ne fait pas part à la femme du boucher. Son désir est de s’identifier à son amie hystérique qui paraît dans les associations puisque, bien que maigre, elle plaît à son mari, celui-ci appréciant plutôt les grosses. Lacan prolonge donc cette interprétation par une troisième qui continue la seconde, en soulignant que la rêveuse s’identifie aussi dans ce rêve à son mari, car elle souhaite répondre à la question de toute hystérique, qu’elle pose en faisant l’homme : comment un homme peut-il désirer ce qu’il n’aime pas? Enfin, Lacan toujours, ajoute que la dame s’identifie au saumon lorsqu’il évoque le filet de gaze qui sépare les tranches de poisson fumé dont il fait l’analogue du voile masquant le phallus qu’on vient de découvrir dans les fresques où apparaît le démon de la pudeur sur les murs de la villa des mystères à Pompéi. Ce qui fait quatre. Comment par conséquent serrer de plus près le fait qu’un rêve est susceptible de quatre interprétations différentes qui sont chacune aussi justes et coordonnées entre elles, si ce n’est que de se saisir de ces coupures condensant la désorientation de la surface d’empan d’une chaîne faite de plusieurs ronds. Quatre coupures valent pour trois ronds d’après notre algorithme et le petit calcul que nous venons d’indiquer. La coupure, c’est ce que doit tracer l’interprétation du nœud qui n’a pas à être exhaustive, passer par toutes les zones; il lui suffit de résumer la désorientation en réorientant l’ensemble de la surface donnant leur sens aux zones de la partie non-nœud qu’elle ne traverse pas. Nous reprenons immédiatement le résultat, touchant au nombre de coupures, dans le chapitre suivant, afin d’interpréter la variation du nombre de la coupure en termes d’enlacements. a6 - Le cas des présentations alternées Dans le cas de la surface d’empan minimum d’une présentation alternée, nous sommes amenés à distinguer deux familles de nœuds par opposition aux non-nœuds isolés par le second temps de notre algorithme. Ces deux familles sont définies en fonction de la parité de la coupure. La coupure passe par un certain nombre de demi-torsions. Nous appellerons ce nombre le nombre de la coupure et nous le noterons k. Parité de la coupure Nous appellerons parité de la coupure le caractère pair ou impair du nombre de la coupure. Si la coupure est impaire, le nœud alterné est de la même famille que le trèfle. Si la coupure est paire, le nœud alterné est de la même famille que le nœud de Listing.
Fig. 51 Les non-nœuds déjà rencontrés ont une coupure nulle, de même parité que les listings29. Présentations équilibrées Lorsqu’il est équilibré, l’unicité de la famille à laquelle appartient le nœud considéré, quand il est alternable et dans sa présentation alternée, est aussi assurée. Si les deux surfaces d’empan duales l’une de l’autre sont unilatères, il est facile de démontrer que, dans les cas équilibrés, la coupure de l’une et celle de l’autre seront de même parité.
Fig. 52 En effet, si nous reprenons, à cette occasion, la formule élémentaire du nœud que nous avons établie à la suite de notre premier temps30 : P + V = C + 2 Et à nous rappeler, comme nous l’avons défini dans le même temps, que les nœuds équilibrés sont tels que P = V. Dans ces conditions, cette formule devient : 2P = C + 2 ou 2V = C + 2 Ainsi, il est facile de constater, dans le cas particulier des nœuds équilibrés, le nombre de croisements est pair : C = 2 (V – 1) La partie nœud et la partie non-nœud sont donc de même parité, puisque leur somme est un nombre pair. Cette précision assure la définition de la parité de la coupure des nœuds et des chaînes équilibrés. Ces nœuds et ces chaînes appartiennent bien à une famille, sans équivoque possible. Nous regroupons dans un tableau le vocabulaire adopté en partant de la distinction reçue en mathématique entre les nœuds faits d’un seul rond et les chaînes constituées de plusieurs ronds. Nous substituons à ce critère portant sur l’unicité ou la multiplicité des ronds un autre trait distinctif relatif à la nécessité de la coupure selon que cette nécessité s’impose ou ne s’impose pas. Nous appelons nœuds les cas alternés où la coupure est nécessaire, ceci à entendre comme un : “il y a du nœud”. Nous parlerons de nœuds propres dans le cas fait d’un seul rond, et de nœuds impropres lorsqu’il y a plusieurs ronds. Nous appelons non-nœuds les cas alternés dont la surface d’empan minimum est bicolorable, c’est-à-dire ne nécessitant pas de coupure.
Terminologie pour les chaînes et les nœuds alternables de 1, 2 et 3 ronds dans leur présentation minimale alternée. Notre terminologie est particulièrement pertinente dans les cas alternés faits de un, deux ou trois ronds. Nous donnons dans ce qui suit les raisons qui étayent cette désignation des objets, et nous traiterons de la généralisation à un nombre plus important de ronds. Nous adoptons dans les cas non alternés la distinction formulée grâce au syntagme, présentation comme un nœud, là où la coupure est nécessaire, et, présentation comme un non-nœud, là où la coupure n’est pas nécessaire, lorsqu’il existe un coloriage ne nécessitant pas de coupure. La conséquence principale de ces trois temps de l’algorithme est que chaque nœud propre et chaque chaîne alternable appartient à une famille portant un nom de façon univoque, et dont nous nous servirons dans notre description de la multiplicité des nœuds et des chaînes alternés. Ceci du fait que : — la parité de la coupure est fixe pour les chaînes faites de plusieurs ronds; — la parité de la coupure est fixée pour les nœuds propres et les chaînes ayant une surface d’empan minimale et une seule (nœuds et chaînes non équilibrés : P > V); — la parité de la coupure est fixe pour les nœuds propres et les chaînes équilibrés (P = V) quelle que soit la surface d’empan minimale choisie parmi ses deux surfaces d’empan duales l’une de l’autre. Les nœuds propres et impropres se répartissent en deux familles dites Trèfle et Listing. Les non-nœuds se répartissent, selon l’unicité ou la multiplicité du nombre de ronds, en nœuds de Lacan et en Enlacements. L’existence de nœuds impropres parmi les chaînes couramment désignées ainsi mérite quelques précisions, ce dont nous voulons traiter maintenant en considérant la question de la variation de la coupure dans les cas faits de plusieurs ronds. Trouvez en trois temps et peu de mouvements, une coupure d’un nœud ou d’une chaîne, lorsque cela est nécessaire. Par exemple, les trois temps dans le cas du nœud 62 :
Fig. a Effectuez le même exercice pour chacun des nœuds et chaînes suivants :
Faites attention aux figures b et c. Reportez-vous à l’exercice suivant si vous éprouvez la nécessité d’explications. e2 - Passage de la coupure dans les plis 1. Transformez le dessin d’une surface d’empan donné dans cet exercice, en faisant apparaître des plis à la hauteur de chaque demi-torsion31. Vous pouvez vérifier, dans cet exercice, comment la coupure passe dans un pli et comment les couleurs se répartissent à la hauteur des croisements.
2. Constatez comment passe la coupure dans les plis et vérifiez qu’elle peut y passer deux fois afin de réunir en un seul cercle les deux composants de la coupure du nœud 940 dont vous aurez déterminé le coloriage au cours de l’exercice précédent.
© 1999 Topologie En Extension . Tous droits de reproduction et de représentation réservés. Tous les textes, dessins et graphiques reproduits dans cet ouvrage sont protégés par des droits de propriété intellectuelle détenus par Topologie En Extension. Par conséquent, aucun de ces éléments ne peut être reproduit, modifié, transmis, rediffusé, traduit, vendu, exploité commercialement ou réutilisé de quelque manière que ce soit sans l'accord préalable écrit de Topologie En Extension. |
||||||||||||||||||||||||||

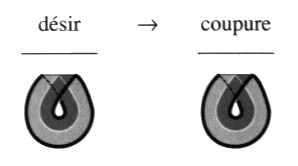

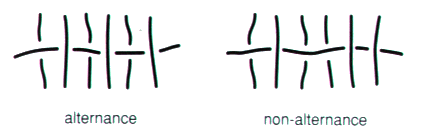
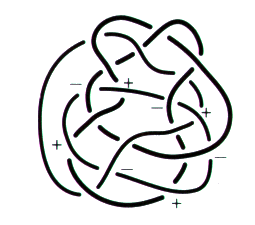
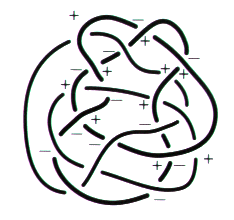
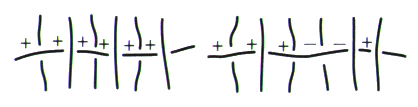
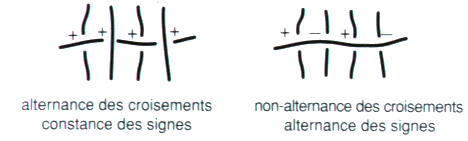
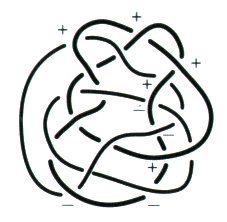
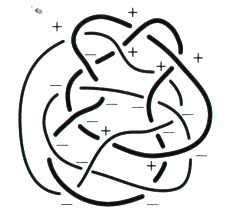

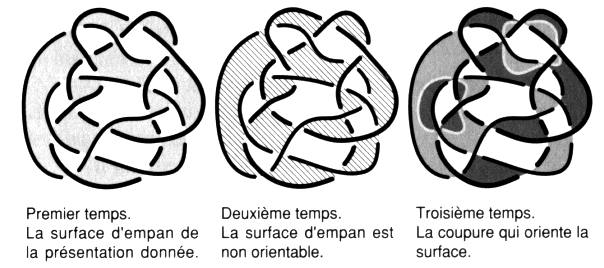

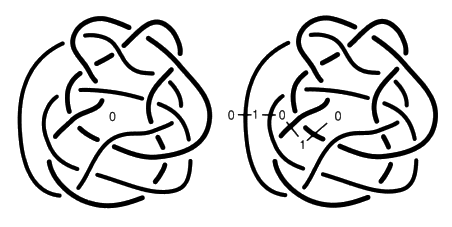
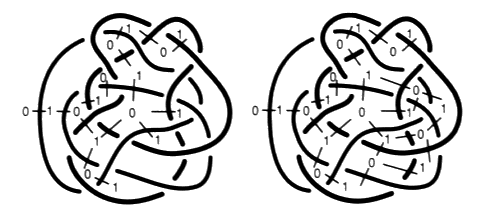
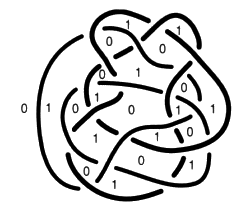
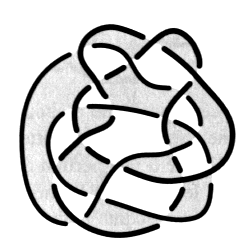


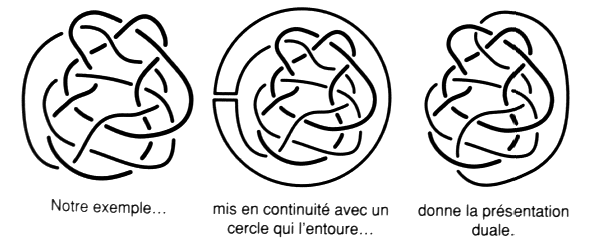
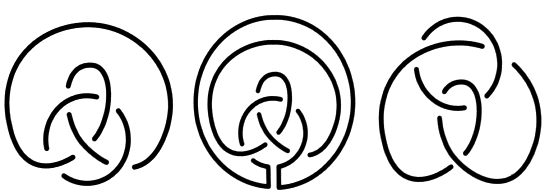
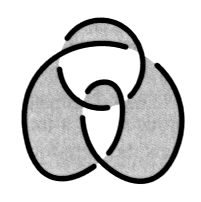

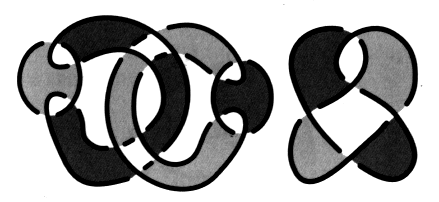
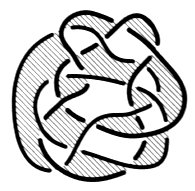
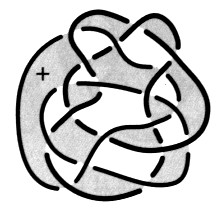
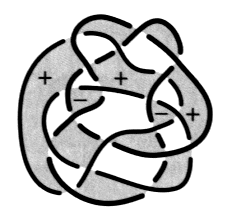
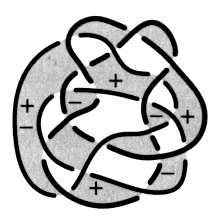
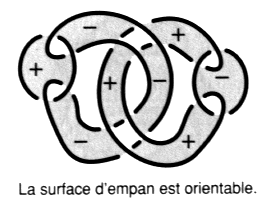
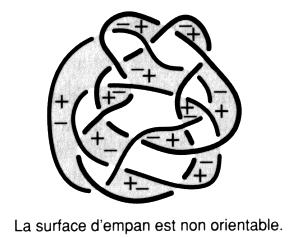
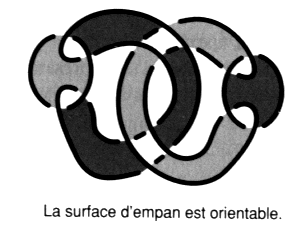
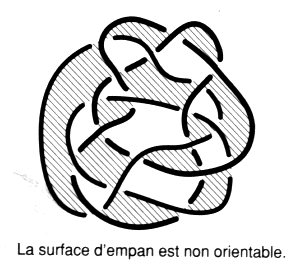

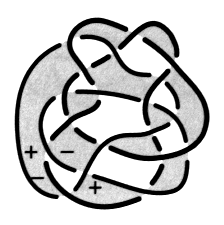


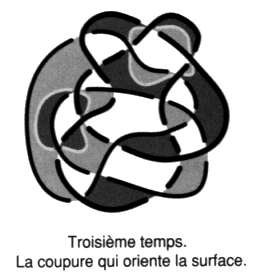

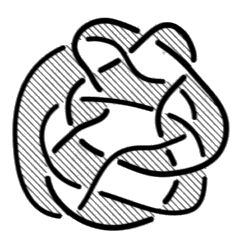
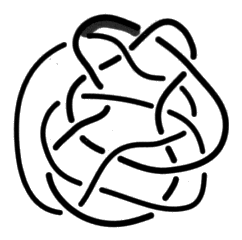

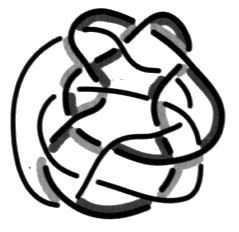






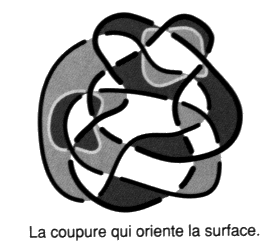
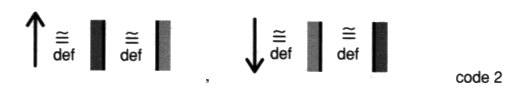



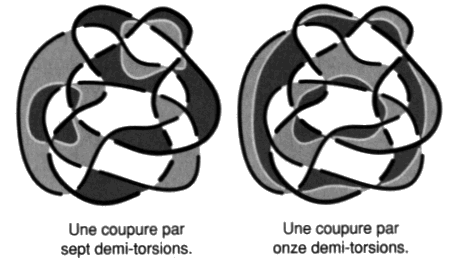
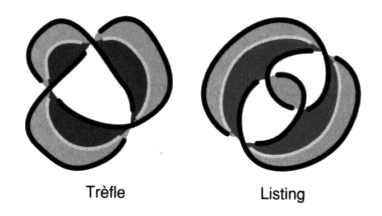
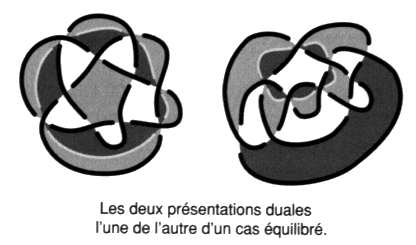

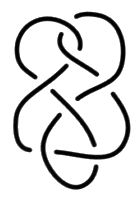 Fig. b
Fig. b 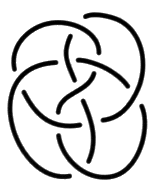 Fig. c
Fig. c  Fig. d
Fig. d 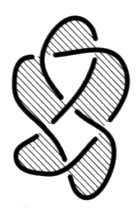 Fig. e
Fig. e  Fig. f
Fig. f