Chapitre III Le nœud est un accomplissement de coupure Quand on a suivi un étroit sentier et que l’on arrive sur une hauteur d’où l’on découvre en diverses directions des perspectives très vastes, on s’arrête et l’on se demande de quel côté l’on se tournera d’abord. C’est le sentiment que nous éprouvons après avoir construit l’algorithme qui faisait défaut pour les chaînes en tant qu’elles intéressent plus d’un rond de ficelle. Nous nous trouvons dans la pleine lumière d’une découverte soudaine. Il est bien sûr que nos procédures ne généralisent pas le lemme de Dehn, puisque notre algorithme ne répond pas directement à la question de savoir si le nœud ou la chaîne sont ou non triviaux, c’est-à-dire constitué de ronds non noués et dispersés. Nous en déduirons par la suite un procédé graphique qui nous assurera de l’existence d’un nombre caractéristique minimum, mais dont la valeur reste non décidée. La première indication, fournie par cette pratique, résout la difficulté qui peut être éprouvée à tenter de s’orienter dans le plan de la mise à plat de l’objet. Elle indique, quelle que soit la disposition du schéma plat dans le plan, qu’il s’agit d’y distinguer des parties, au lieu que de chercher à s’orienter en termes de gauche et de droite, de haut et de bas, ou par rapport à quelque repère fixé à l’avance, comme en géométrie analytique. La présentation de l’objet n’est pas pour autant un chaos de traits discordants issu d’une fantaisie tracée au hasard, nous préciserons quels en sont les éléments et leur mode de montage dans les chapitres suivants1, grâce au fait qu’il s’y accomplit une coupure. Nous voulons préciser ici le registre de ce que nous entendons par cet accomplissement. Il faut noter une première chose à propos de cette distinction de parties pour une présentation et un coloriage donné. Dans les chaînes faites de plusieurs ronds, ces parties s’enchevêtrent selon la variation des coloriages que l’on peut réaliser à leur occasion. Nous constatons que la variation se fait selon un système de coupure, qui s’oppose à son accomplissement ayant plutôt trait au non-nœud contenu dans la chaîne qu’à son nœud. Nous commencerons par rendre compte de la variation de la coupure au moyen d’un comptage, puis du mouvement de la coupure en affinant ce calcul dépendant des mouvements élémentaires de la théorie. La mise en valeur des non-nœuds, caractérisée par l’absence de coupure, révélera le registre pertinent de ce que nous appelons son accomplissement. Cet accomplissement apparaîtra de manière certaine au travers de formules arithmétiques. Nous tenterons dans notre chapitre suivant de le précipiter d’une manière lisible dans les dessins. 1. Passage de la coupure dans un pli Il nous reste une précision à apporter en supplément au chapitre précédent. Le tracé de la coupure dans les dessins de schémas plats (diagrams) peut faire difficulté au lecteur lors du passage de celle-ci dans les torsions de surface. Il y a là une répartition des couleurs qui mérite d’être commentée.
Fig. 1 Pour cela, il nous faut nous reporter à ce que nous montrions dans le volume précédent consacré aux surfaces2. Nous y expliquions, en effet, que le dessin d’une torsion d’étoffe est l’épure d’un dessin de pli de ruban d’étoffe. Le pli peut être rétabli à la hauteur de chaque torsion. Il suffit d’effectuer cette transformation, elle correspond à un calcul, afin de vérifier la pertinence de nos coloriages. Considérons un croisement d’éléments de corde, pourvu d’une surface d’empan. Nous ajoutons une ligne de pli et faisons paraître en pointillé la ligne de bord, qui passe dans le pli en dessous du ruban, comme nous l’expliquions dans notre deuxième fascicule.
Fig. 2 Dans le cas d’un ruban orientable, il y a un échange des couleurs de la face visible lors du passage d’un pli.
Fig. 3 Dans le cas d’un ruban participant d’une surface non orientable, réorientée par la coupure, nous pouvons vérifier quel est le trajet de la coupure :
Fig. 4 et, sur le dessin avec un pli, expliquer beaucoup mieux la répartition des couleurs dans la torsion, du fait qu’elles sont toujours adossées l’une à l’autre dans une surface bilatère. Il se voit que nous pouvons adopter, pour la coupure, le même principe imposé dans la mise à plat des nœuds, principe qui veut que jamais plus de deux consistances de ligne ne se croisent en un même point.
Fig. 5 Ce principe n’est pas respecté dans l’épure de présentation en termes de torsion pour des raisons de commodités, puisqu’il va principalement être question de compter les croisements par où passe la coupure. Dans le cas des chaînes faites de plusieurs ronds, la reprise du procédé de notre troisième temps algorithmique donne lieu à plusieurs possibilités. De ce fait, il existe plusieurs coupures différentes, dont le nombre k, qui est attaché à chacune, peut varier. Il s’agit des différents nombres de croisements par où passent ces coupures. La parité de ces différents nombres de la coupure est constante pour une même présentation. Nous distinguerons cette variation de la coupure pour une même présentation du mouvement de la coupure au travers des changements de présentation. Notre exemple, constitué de trois ronds, présente quatre coupures qui réorientent la surface. Ces nombres peuvent s’écrire en un répartitoire :
Ce répartitoire les fait correspondre à la disposition des dessins suivants :
Fig. 6 Mais il nous faut être attentif au fait que les croisements peuvent ne pas être alternés, comme dans le cas que nous considérons ici. Si nous formulons ce fait, en notant comme dans notre récit préliminaire, grâce à deux signes opposés, en plus (+1) et en moins (–1), les croisements non alternés entre eux.
Fig. 7 Ces nombres attachés à chaque coupure se trouvent modifiés. Dans notre exemple, la coupure à laquelle est attaché le nombre 7 passe par quatre croisements présentant une alternance (+) différente des trois autres (–). Dans ce même exemple les coupures parcourant 11 croisements passent curieusement par quatre croisements présentant une alternance notée (+) différente des sept autres (–). Ces nombres caractéristiques des coupures se trouvent, par conséquent diminués et orientés. Nous obtenons ainsi un nouveau répartitoire, correspondant toujours à la disposition des dessins.
Soit: Nous pouvons constater alors, sachant que le nombre d’enlacement d’entre les ronds d’une chaîne, bien connu en mathématique, est le premier chiffrage, le plus simple, qui se prête au calcul, que la différence d’entre les nombres correspondant à ces coupures coïncide avec le nombre d’enlacement de chaque rond avec l’ensemble des autres ronds3. C’est le problème que nous voulons étudier ici afin de l’isoler. Pour plus de précision, il nous faut définir le nombre d’enlacement (linking number) entre les ronds. Ce nombre dépend de l’orientation du sens de parcours le long des ronds de ficelle. Cette orientation des ronds produit une orientation des croisements. Mais, dans le même temps, il va se révéler la nécessité d’une autre orientation des objets. De ce fait, nous donnons en même temps les définitions de ces deux modes d’orientation des croisements. 3. Une autre orientation dans les nœuds et les chaînes Il est courant, depuis les travaux de Tait, comme dans la définition de la vrille (writhe), de noter les croisements d’éléments de ronds orientés grâce à deux signes +1 et –1.
Ceci définit le signe de chaque croisement (crossing sign), que nous appellerons la caractéristique (si) de chaque croisement, compte tenu de l’orientation des ronds, notée i. Il existe une autre orientation des croisements dans une présentation d’objet, en tenant compte cette fois de la distinction des pleins et des vides, qui est indépendante de l’orientation des ronds. Les pleins et les vides sont définis par le premier temps de l’algorithme de lecture du nœud que nous avons proposé. À une présentation (diagram) d’un objet, nous faisons correspondre le choix des pleins et des vides qui attribue la valeur de vide à la zone extérieure (zone infinie du plan), soit encore la zone qui est autour de la présentation. Posons deux signes +1 et –1 pour les deux types de croisements non orientés par le sens de parcours sur les ronds de ficelle, où il est seulement décidé de la différence des pleins et des vides.
Ces deux croisements orientés par les pleins et les vides ne sont plus superposables dans le plan. Nous appellerons ce signe d’incidence +1 ou –1 la torsion (tp) de chaque croisement4. Cette distinction entre l’orientation des croisements par la torsion et l’orientation des croisements par la caractéristique a été peu développée par les mathématiciens jusqu’à une période récente5. Le calcul y trouve moins son compte du fait du caractère global de cette orientation par la torsion, alors que l’orientation par la caractéristique étant localisable à la hauteur de chaque rond. Cette question touche aussi à la représentation et au calcul, elle étaye notre approche par une écriture propre au nœud, exacte dans son tracé, rigoureuse dans son articulation en discours, qui ne peut méconnaître l’écriture algébrique standard. a2 - Quatre types de croisements Ainsi chaque croisement peut recevoir une double orientation dans une présentation d’objet où ont été distingués les pleins et les vides, lorsqu’elle est orientée quant aux ronds. Il y a donc quatre types de croisements.
Principe esthétique La surface, qui sert à définir la torsion, ainsi disposée à la hauteur d’un croisement, nous permet de faire apparaître le coloriage produit par notre algorithme comme convenant à rendre compte de l’orientation des ronds par des couleurs disposées sur le côté de chaque élément de ficelle. Cette correspondance entre l’orientation des ronds et le coloriage des zones donnera lieu à une petite étude séparée6. Nous indexons ces quatre types de croisements par un couple (t, s), où les nombres t et s sont pris dans la paire {+1, –1}. Le premier note la torsion, le second la caractéristique. Notons également p, q, b et d les nombres respectifs de ces quatre types de croisements (+1, +1), (+1, –1), (–1, +1) et (–1, –1) dans une présentation orientée ou colorée. a3 - Trois nombres remarquables Pourvu de cette double orientation, pour une présentation p, où les pleins et les vides sont distingués, et d’orientation quant aux ronds ou de coloriage i, posons : — le nombre des croisements orientés par la torsion : cp = p + q – b – d où p indique le choix de la présentation. — le nombre des croisements orientés par leur caractéristique, soit la vrille (writhe) : vi = p – q + b – d où i indique le choix d’orientation des ronds ou le coloriage pour la présentation donnée. Si Xi et Yi sont deux ronds de la présentation orientés par i, on parle de l’ensemble des croisements mutuels de Xi et Yi, ce qui s’écrit crois (Xi, Yi), et on pose, par définition, le nombre d’enlacement (linking number) de ces deux ronds :
obtenu comme la demi-somme des caractéristiques de leurs croisements mutuels, où si (x) est la caractéristique du croisement x. — On définit ainsi le troisième nombre remarquable dans une présentation, le nombre de chaîne Si, comme la somme des nombres d’enlacement (enl) de rond à rond orientés par la caractéristique. Soit Pi l’ensemble des paires de ronds distincts {Xi, Yi} de la présentation orientée par i, alors :
D’autres définitions Dans une présentation, nous appellerons croisements impropres les croisements mutuels de deux ronds et croisements propres les croisements d’un rond avec lui-même. Ainsi les nœuds propres faits d’un seul rond ne présentent que des croisements propres et il n’est pas question à leur sujet de nombre d’enlacement. Nous dirons que leur nombre de chaîne Si est nul. Il existe des chaînes présentant exclusivement des croisements impropres. Dans le cas le plus général d’une chaîne, la présence de croisements propres et de croisements impropres peut se trouver. Le nombre de chaîne Si est en fait la demi-somme des caractéristiques des croisements impropres de l’ensemble de la présentation colorée. Nous le distinguons des nombres d’enlacement enl (Xi, Yi) respectifs des couples de ronds qui donnent un aperçu plus détaillé de l’état des enlacements de l’objet. À ce propos, nous aurons à considérer deux types de répartitions : Pour une présentation colorée, nous aurons à considérer la répartition des nombres d’enlacement respectifs des couples de ronds. Pour une présentation non colorée, nous parlerons aussi de la répartition des nombres de chaîne Si obtenus à l’occasion de chacun de ses coloriages. a4 - Chiffrage de notre exemple Reprenons le résultat du chiffrage freudien dont nous sommes parti au début du chapitre II. Il rend compte de l’alternance et de la non-alternance des passages de la ficelle dans les croisements. C’est ainsi que nous l’avons obtenu sur l’exemple général déjà choisi dans la présentation p comme un chiffrage de ce fait. Nous pouvons maintenant lui donner un sens.
Fig. 8 Les signes de la première figure correspondent au signe de torsion de chaque croisement de la seconde figure. Ces signes sont définis lorsqu’une surface d’empan de l’objet est déterminée, ils prennent leur sens dès le premier temps de l’algorithme terminé. Encore fallait-il isoler, dans la mise à plat, l’opposition des deux torsions, notées de manière positive ou négative, dans les couples de croisements munis de cette surface. Ainsi pondérés par les pleins et les vides, les croisements ne sont plus tous superposables au travers des déplacements sur le plan. Il y a alors deux types de croisements. Montrons comment obtenir l’effet chiffrable sur cette dernière figure des autres définitions que nous venons de rencontrer. Nous conservons l’exemple général déjà choisi dans la présentation p, maintenant orienté grâce aux coloriages i.
Fig. 9 Il faut se reporter au tableau qui donne les valeurs de la torsion et de la caractéristique des quatre types de croisements et tenir compte du caractère propre ou impropre de chacun d’eux pour déterminer le nombre de chaîne. cp = –5, car il y a sept croisements de torsions positives et douze de torsions négatives (+ 7 – 12 = –5). vi = –7, car il y a, parmi les croisements de torsions positives, trois croisements de caractéristiques positives par où ne passe pas la coupure et quatre croisements de caractéristiques négatives par où passe la coupure d’une part, puis parmi les croisements de torsions négatives, neuf croisements de caractéristiques négatives par où ne passe pas la coupure et trois croisements de caractéristiques positives par où passe la coupure d’autre part (+ 3 – 4 – 9 + 3 = –7). Si = –3, car il y a quatorze croisements impropres et cinq croisements propres. Trois croisements propres sont de torsion positive dans ce cas et deux de torsion négative. Parmi les trois premiers un est de caractéristiques positives — la coupure n’y passe pas — et deux de caractéristiques négatives — la coupure y passe. Parmi les deux autres il y a un croisement de chaque sorte. Nous modifions le calcul précédent en supprimant ces valeurs respectives (+ 2 – 2 – 8 + 2 = –6) puisque nous ne calculons cet indicateur que sur les croisements impropres. La somme des enlacements est par définition égale à la moitié de cette somme (1/2 (+ 2 – 2 – 8 + 2) = –3). Nous pouvons détailler la répartition des nombres d’enlacements mutuels des couples de ronds, en nommant les trois ronds de trois lettres distinctes S, T et J.
Fig. 10 Nous comptons le nombre de croisements impropres de chaque type communs à chaque couple de ronds. enl (S, T) = 1/2 (+ 2 – 2 – 2 + 0) = –1 enl (T, J) = 1/2 (+ 0 – 0 – 4 + 2) = –1 enl (J, S) = 1/2 (+ 0 – 0 – 2 + 0) = –1 Dans ce calcul, les croisements sont de signe positif et négatif en raison de l’orientation produite par la caractéristique. Sur notre exemple, nous pouvons vérifier que la somme de ces trois comptages donne bien le résultat obtenu plus haut, Si = –3, mais nous remarquerons qu’il est plus aisé de le trouver directement par le calcul de la demi-somme globale des caractéristiques des croisements impropres. Muni de ces définitions, afin de traiter de la variation de la coupure, reprenons maintenant à partir d’une remarque relative à la différence qui existe entre les croisements propres et les croisements impropres, dans l’effet que produit, à la hauteur de ces croisements, un changement d’orientation ou de coloriage. 4. De la variation de la coupure Nous venons de préciser la distinction qu’il y a entre les croisements propres et les croisements impropres. Cette nuance nous conduit à formuler un principe très pratique dans la recherche des différentes coupures d’une présentation donnée, lorsque nous connaissons déjà l’une d’entre elles. a1 - Différence entre les croisements propres et impropres Ce principe dépend de la réaction différente des croisements propres et impropres à la variation de la coupure. Commençons par discuter cela. Croisements impropres À la hauteur d’un croisement impropre, si nous changeons l’orientation d’un des ronds, la caractéristique change, et par conséquent le type du croisement change aussi. En effet, les signes caractéristiques forment par définition un simple couple et ses deux termes se différencient lors du changement de sens d’un seul des éléments de ficelle constituant le croisement considéré. Ce changement n’affecte pas la torsion. Ainsi, dans le cas d’un croisement impropre, lorsqu’un seul élément de ficelle change de sens, la caractéristique change et par conséquent le type de croisement est modifié en restant de même signe de torsion. S’il était de type nouage, avec coupure, il devient de type non-nouage sans coupure, deux cas peuvent se produire.
Inversement, s’il était de type non-nouage, sans coupure, il devient de type nouage, avec coupure. Pour le vérifier, il suffit de considérer rétroactivement les mêmes couples de croisements donnés en exemple. Croisements propres Les croisements propres ne changent pas de caractéristique ni de type de croisement dans un changement d’orientation du rond considéré. Les deux éléments de ficelle d’un croisement propre participent du même rond. Lorsque l’orientation du rond en question change, les deux éléments de ficelle changent de sens simultanément. Il y a donc un double changement de sens à la hauteur de ce croisement propre, ce qui revient à ne rien changer. Comme nous venons de le voir, du fait de l’existence d’un seul couple d’opposition des signes de caractéristique dont les termes s’échangent lors du changement d’orientation d’un seul élément de ficelle, un double changement de sens à la hauteur d’un croisement produit une involution et ne modifie pas sa caractéristique. Par conséquent, à la hauteur d’un croisement propre, si nous changeons l’orientation du rond, la caractéristique ne change pas, et comme ce changement n’affecte pas la torsion, il suit de cela que le type de croisement ne change pas. S’il était de type non-nouage, sans coupure, il le reste.
S’il était de type nouage, avec coupure, il le reste aussi.
Nous déduisons de ce fait un principe. Pour obtenir à partir d’une coupure donnée, une autre coupure par changement de coloriage ou d’orientation d’un rond, seuls ses croisements impropres d’avec les autres ronds changent de type. Ce principe dit aussi que la variation de la coupure suit le changement de type des croisements impropres. Donnons un exemple de l’usage de ce principe dans le cas général que nous avons choisi.
Fig. 11 Si nous suivons le parcours du rond qui change d’orientation, marqué en gras, là où la coupure passait dans les croisements impropres auxquels il participe, elle ne passe plus, et elle passe par ceux où elle ne passait pas. a3 - Variation topologique de la coupure Nous pouvons montrer avec plus de précision ce qui se passe lors du changement d’orientation d’un rond, lorsque la coupure varie. D’après notre troisième temps algorithmique, la variation de la coupure est produite par un choix différent des couleurs réparties le long d’un rond de la chaîne. Prenons le coloriage de notre exemple auquel correspond une coupure k1p.
Fig. 12 Le changement de coloriage d’un rond peut être explicité par une coupure k12 longeant ce rond. Nous changeons dans ce cas l’orientation d’un rond, choisissant un autre rond différent de l’exemple précédent, toujours marqué en gras, et accompagné de tout son long de la coupure k12.
Fig. 13 Nous mettons en continuité cette coupure k12 avec la coupure k1p de départ, pour obtenir la seconde coupure k2p.
Fig. 14 Nous ne justifions pas autrement ce procédé que par le fait qu’il est cohérent avec les coloriages7. Nous obtenons ainsi une explication, au sens d’un dépliage, de la variation de la coupure, et nous pouvons envisager de calculer la différence entre ces deux nombres de la coupure afin de chiffrer cette coupure k12 intermédiaire. Mais nous ne suivrons pas cette voie pour l’instant, et nous traiterons une question d’importance éminente dans notre propos. 5. De l’accomplissement de la coupure Avec ces conventions, nous pouvons écrire une définition et un théorème principal. Pour une présentation d’un nœud ou d’une chaîne orientée par la torsion, dont les ronds sont non orientés, nous appellerons la moyenne des nombres de la coupure le nombre Sp obtenu pour une orientation i quelconque des ronds de cette présentation : Sp = 1/2 (cp – vi) + Si Résultat principal i – Pour une présentation p donnée d’un nœud ou d’une chaîne et pour une orientation i quelconque de cette présentation, nous pouvons écrire la relation suivante : cp – 2Sp = vi – 2Si = h ii – Le nombre Sp est orienté par la torsion et est indépendant des coloriages (des orientations) des ronds qui forment le nœud ou la chaîne. D’après la définition de Sp, la relation qui forme la première partie de cet énoncé, est une proposition aisée à établir. Il faut démontrer l’indépendance de Sp par rapport au coloriage (à l’orientation) i pour établir la deuxième partie de ce résultat principal. Pour démontrer cela, nous allons recourir à la définition du nombre h qui apparaît dans notre expression formelle et à son indépendance relative à l’orientation i et à la présentation p. En effet, vi et Si sont des invariants des isotopies régulières, mouvements de Reidemeister8 M2 et T3. Du fait de la définition de vi, par les caractéristiques de l’ensemble de tous les croisements de la présentation, et de Si, par les caractéristiques des seuls croisements impropres, le nombre h est bien défini comme la somme des caractéristiques des seuls croisements propres. Nous appellerons vrille propre ce nombre h et nous pouvons noter au passage le résultat supplémentaire suivant. Vrille propre 1. La vrille propre h = vi – 2Si est un invariant des présentations de nœuds ou de chaînes, pour les isotopies régulières pratiquées sur la sphère. C’est dire que h est indépendant de la présentation p, tant que nous ne créons pas et ne supprimons pas de boucles, celle-ci ne change que du fait des isotopies régulières composées de M2 et T3. Mais afin de démontrer notre résultat principal, nous avons recours à un autre résultat partiel conséquence de ce que nous avons déjà constaté. 2. La vrille propre h est indépendante des coloriages des ronds qui forment le nœud ou la chaîne. Comme nous l’avons montré plus haut à propos des croisements propres, ceux-ci ne changent pas de caractéristique lorsque nous changeons de coloriage. Ainsi, grâce à ce dernier lemme, nous savons que le nombre h étant indépendant du coloriage — or le nombre cp étant lui-même indépendant du coloriage i, par définition il ne dépend que de la torsion — nous pouvons conclure que le nombre Sp = 1/2 (cp – h) est bien indépendant du coloriage et ne dépend que de la torsion, ce qu’il nous fallait démontrer. a2 - Chiffrage de notre exemple Afin de nous exercer à la lecture de ce résultat principal dans les dessins, revenons à notre exemple. Les valeurs de vi et de Si se calculent sur les figures, en ayant recours à leur définition, comme la valeur de cp = –5, qui ne dépend pas du changement de coloriage mais seulement de la torsion, or le nombre de torsion des croisements ne change pas entre ces dessins. Il se trouve que h = vi – 2Si = –1, il ne varie pas dans les quatre cas comme le dit notre deuxième lemme, et de fait sa valeur se justifie ici car il y a trois croisements propres de torsion positive et deux croisements propres de torsion négative dans ce cas. La moyenne des nombres de la coupure Sp =1/2 (cp – h) = –2, par définition, est bien indifférent aux coloriages i, et notre relation se vérifie à l’occasion des quatre coloriages.
Fig. 15 Mais il est plus intéressant de justifier le nom de moyenne des nombres de la coupure donné à Sp. Nous commenterons ce quatrième chiffre, après être revenus aux variations de la coupure, c’est-à-dire au problème dont nous étions partis. Nous avions dressé le répartitoire des nombres de croisements par où passe la coupure en tenant compte de la non-alternance des croisements. Cette non-alternance s’exprime maintenant pour nous en termes de torsions opposées, et notre exemple présente des torsions négatives en plus grand nombre. Notre répartitoire orienté par la torsion devient :
Dans le cas du coloriage dessiné à gauche, kip = –3, la coupure passe par onze croisements, dont quatre sont de torsion opposée aux sept autres. Nous nous proposons de définir le nombre de la coupure kip par la différence de ces deux nombres : kip = 4 – 7 = –3 Cette définition du nombre de la coupure en fonction du nombre de torsion donne le résultat escompté dans les trois autres cas. Ainsi, le nombre de la coupure kip est la somme des valeurs des croisements orientés par la torsion, par où passe la coupure. En d’autres termes, nous dirons pour résumer cette définition, que le nombre de la coupure vaut : kip = q – b sachant que q et b sont les nombres respectifs des croisements de type (+1, –1) et (–1, +1). Ce nombre est en relation avec deux des indicateurs définis plus haut. Le nombre de la coupure kip vérifie la relation : kip = 1/2 (cp – vi) Cette relation s’éprouve facilement par un simple calcul compte tenu de la disposition des signes des nombres respectifs des quatre types de croisements, dans ces deux indicateurs : cp = p + q – b – d vi = p – q + b – d Ainsi : cp – vi = 2q – 2b = 2 (q – b) = 2 kip q et b correspondent aux croisements par où passe la coupure, pourvus ici de leur signe de torsion, d’où la relation proposée. Nous appellerons partie nouage cette expression (q – b); c’est le nombre de la coupure. La partie non-nouage est aussi caractérisée par un nombre résultant d’une expression : – k*ip = p – d. Il s’agit de l’opposé du nombre de la coupure duale9. Dans la présentation duale, la torsion s’inverse ainsi, par exemple le nombre des croisements orientés par la torsion dans la présentation duale pourvue de sa surface d’empan vaut c*p = cp* = – cp et la partie non-nouage vérifie les mêmes propriétés que le nombre de la coupure dans la situation duale : k*ip = 1/2 (c*p – v*i) = 1/2 (– cp – vi) La caractéristique ne change pas dans la situation duale et par conséquent la vrille ne change pas, donnant l’expression proposée : – 2 k*ip = cp + vi = 2 (p – d). a4 - Variation arithmétique de la coupure Ce nombre de la coupure dépend de la torsion et des coloriages. Pour une orientation i d’une présentation donnée d’un nœud ou d’une chaîne, notre théorème principal nous assure que le nombre de la coupure kip vérifie la relation suivante : kip = 1/2 (cp – vi) = Sp – Si Nous avons donc le résultat suivant qui résout notre problème. Le nombre de la coupure kip vérifie la relation : kip = Sp – Si Ainsi pour une présentation donnée, la variation de la coupure en fonction des coloriages suit en son nombre la variation de la valeur de Si. Cette conséquence se déduit immédiatement de notre corollaire principal puisque Sp est indépendant du coloriage i. Le répartitoire des nombres de la coupure est donc un transformé du répartitoire des nombres de chaîne Si. La transformation entre ces répartitoires est donnée par la formule kip = Sp – Si, elle consiste à inverser leurs signes et à les translater de la longueur Sp. Dans notre exemple où Sp = –2, nous pouvons interpréter maintenant la répartition des valeurs de la coupure.
Ces résultats éclairent le fait que nous parlions, à propos du chiffre Sp, de l’expression de la moyenne des nombres de la coupure10, ce qu’il est en effet, comme nous le démontrons maintenant. a5 - Première interprétation de Sp Nous interprétons Sp comme étant la moyenne des nombres de la coupure variant au travers des différents coloriages. Pour une chaîne de r composants (ronds), il y a n = 2r coloriages possibles. Pour les n coloriages d’une présentation d’un nœud ou d’une chaîne, l’expression de la moyenne des nombres de la coupure s’écrit :
Calculons la valeur de cette expression, en utilisant notre corollaire qui dit que kip = Sp – Si. Ainsi, puisque Sp est indépendant des coloriages i :
Nous utilisons alors une nouvelle proposition. Dans un objet quelconque, la somme des nombres de chaîne répartis d’entre les coloriages est nulle.
Cette dernière relation est facile à établir à partir de la définition donnée plus haut des Si, en fonction des caractéristiques si, et sachant que le changement d’orientation d’un rond inverse le signe caractéristique de chacun des croisements impropres de ce rond avec les autres ronds. Ainsi, chaque caractéristique apparaît à chaque fois en nombre pair, pourvu de signes opposés dans chaque couple, ce qui assure leur annulation mutuelle. Grâce à cette proposition, nous pouvons déduire que :
Ce que nous voulions vérifier pour notre interprétation. La moyenne des nombres de la coupure Sp peut être encore interprétée au travers des enlacements et des mouvements de la théorie, qui assure l’identité des objets au travers des changements de présentation; nous allons étudier cela dans les chapitres suivants, mais pour le démontrer et le calculer, nous devrons préciser au préalable quelques définitions. a6 - De l’accomplissement de la coupure Nous avons ainsi résolu, en arithmétique, le problème de la variation de la coupure et nous pouvons alors le distinguer de ce que nous appelons son accomplissement. Ce que nous appelons, dans notre titre, l’accomplissement de la coupure ne saurait être réduit à la variation du nombre de la coupure, pour la raison que la variation du nombre de la coupure c’est la variation des nombres de chaîne, soit la répartition des enlacements et, comme nous le montrons par la suite, c’est le non-nœud contenu dans la chaîne dans les cas de un, deux et trois ronds. Ceci est notre premier point. En second lieu, si nous soulignons dans notre relation principale : cp – 2Sp = vi – 2Si que chacun de ses membres est orienté respectivement par la torsion et par la caractéristique, nous dirons que le nombre de la coupure s’accomplit comme une articulation entre ces deux orientations. Cette articulation est écrite par la formule condensée : kip = 1/2 (cp – vi) = Sp – Si Le nombre kip dépend des deux orientations, au contraire de la vrille propre h qui est indépendante des deux orientations. Ainsi l’accomplissement arithmétique et formel de la coupure est cette articulation où, pour le dire autrement, il y a une sorte d’oscillation portée par la coupure, qui tient de l’une et de l’autre d’entre nos deux orientations et réalise une pulsation de l’un à l’autre des membres de notre relation principale. Si nous associons à la mise à plat
d’un objet avant que d’effectuer notre algorithme, l’index Notre expression écrite en arithmétique du nœud articule la relation du sujet barré par la coupure produite par le coloriage à cet objet dit petit a, cause de son désir. Le nombre de la coupure vient comme le manque, noté –j, osciller entre les deux termes de cette relation, nos deux orientations, et la coupure de s’accomplir dans nos présentations de nœuds11. Par contre, dans nos dessins, l’accomplissement de la coupure paraît dans son registre propre qui est topologique. En effet, l’interprétation topologique du nombre de la coupure kip est donnée grâce à notre algorithme. L’accomplissement topologique de la coupure, le nœud, se produit dans l’espace nodal, pour un, deux et trois ronds12. Il nous faut donc distinguer entre l’accomplissement de la coupure dans l’espace du nœud et son écriture dans les formules alors que cette écriture reste la meilleure indication de cet accomplissement. La question la plus passionnante reste d’apprécier le lien entre les catégories de Lacan une fois constatée cette présence dans le champ du nœud, d’une structure avérée dans le champ freudien. Nous y revenons dans nos Appendices (chapitre II) à propos du calcul des polynômes de nœuds. Nous aurons encore, par la suite, à distinguer cet accomplissement de la coupure du mouvement de la coupure qui rend raison de l’interprétation de Sp au travers des enlacements et des mouvements de la théorie, à la manière de ceux de Reidemeister, pour condenser notre propos sur le nœud. Il reste d’un point de vue technique que la constance de la coupure révèle l’absence d’enlacement, soit un type de chaînes originales caractéristiques du nœud qui échappent au simple calcul du nombre d’enlacement, celui-ci restant aveugle au nœud. L’ensemble de ces considérations et de ces résultats nous mène à adopter le terme de Nœuds impropres pour les chaînes à coupures constantes, qui se résume dans cette condensation de Chaînœuds (linknots) que nous emploierons à leurs propos. En voici un exemple particulièrement élémentaire avec le Nœud borroméen et ses quatre coupures.
Fig. 16 Ces chaînœuds ne contiennent aucun enlacement. Pour justifier notre façon de dire, soulignons que les nœuds propres sont à coupure constante, du fait d’être constitués d’un seul élément de corde. Par conséquent, il nous paraît remarquable que certaines chaînes, faites de plusieurs ronds, présentent une constance du nombre de la coupure qui les rend analogues sinon homologues aux nœuds propres, renouvelant par là la distinction du un et du multiple, comme nous l’étudierons dans notre dernier chapitre. Notre propos, dans la suite, consiste à ne pas laisser cette homologie en l’état et de la fonder comme une structure. 7. De la répartition des enlacements Nous disposons déjà de la formule kip = Sp – Si (corollaire principal) qui exprime la variation arithmétique de la coupure en fonction de la variation des nombres de chaînes. Nous voulons montrer que nous pouvons traiter des enlacements dans les chaînes orientées seulement par la torsion, c’est-à-dire indépendamment d’un coloriage choisi. Il est nécessaire de partir des chaînes orientées par un coloriage afin de calculer, selon la définition correcte du nombre d’enlacement, ce qu’il y a d’enlacement dans une chaîne. À la chaîne orientée par la torsion, à gauche de notre figure, correspond une répartition des nombres de chaîne dispersé d’entre ses différents coloriages. Dans notre exemple où r = 3 :
Fig. 17 Une quelconque des chaînes colorées, à droite de notre figure, présente une répartition des nombres d’enlacement d’entre les couples de composants et un nombre de chaîne obtenu comme la somme de ces nombres d’enlacement. Parmi ces présentations colorées, nous passons de l’une à l’autre en inversant le sens de parcours ou la répartition des couleurs sur un ou plusieurs ronds. Nous nous proposons de commencer par une étude de la relation qui existe entre les répartitions des nombres d’enlacement de rond à rond, pour les chaînes colorées, et la répartition des nombres de chaîne, pour une chaîne non colorée leur correspondant. Il est aisé d’écrire l’ensemble du chiffrage de ces différents cas, afin d’étudier les permutations de signes et les correspondances qui s’en déduisent. À une chaîne de r ronds non colorée correspond 2r coloriages qui donnent des résultats différents lors du calcul des nombres d’enlacement. Nous notons C l’ensemble (de cardinal r) des composants et nous indexons les nombres de chaîne Si par les sous-ensembles de C, c’est dire que i Î P (C), de telle manière que pour une orientation quelconque fixée, notée ø, l’orientation i est obtenue en changeant le sens de parcours des composants appartenant à i. Les nombres de chaîne ainsi obtenus sont bien au nombre de 2r. Les coloriages produisent deux à deux la même coupure, avec la simple inversion globale des couleurs. Nous disposons donc de la relation Si = S¬ i, où ¬ i désigne le complémentaire ensembliste de i dans C. Il y a donc 2r –1 nombres de chaîne à distinguer éventuellement différents qui sont des combinaisons linéaires à coefficients dans {+1, –1} des nombres d’enlacements de tous les couples de composants. Par conséquent il y a 2r –1 nombres de coupure à distinguer. a1 - Des chaînes orientées par la caractéristique Nous parlerons d’une répartition des nombres d’enlacement pour une orientation donnée la distribution des nombres d’enlacement répartis entre les couples de ronds. Il s’agit de la répartition des nombres définis pour une orientation i donnée par l’expression :
Il nous est plus pratique parfois de noter ce nombre multiplicativement XiYi. Définissons une première relation entre les chaînes orientées par la caractéristique ou colorées. Renl-équivalence Deux chaînes de présentations colorées respectives S1i et S2j sont dites Renl-équivalentes, si et seulement s’il existe une bijection f des composants de S1i vers ceux de S2i, telle que pour chaque couple de composants (Xi, Yi) de S1i et, par conséquent, pour chaque couple (f (Xi), f (Yi)) de composants de S2j, l’égalité : enl (f (Xi), f (Yi)) = enl (Xi, Yi). soit vérifiée. Dans ce cas, nous dirons qu’elles ont la même répartition des nombres d’enlacement entre leurs ronds respectifs, et leurs nombres de chaîne respectifs sont égaux : Si = Sj. Cette relation est une relation d’équivalence entre chaînes colorées. Voici un exemple de deux objets Renl-équivalents :
Fig. 18 Pour une même répartition des nombres d’enlacement entre deux chaînes colorées, nous trouvons le même nombre d’enlacement d’entre les couples de ronds de chacune d’elles et, du même coup, le même nombre de chaîne pour ce coloriage. Pour les différents coloriages Dans le cas où S1i et S2j sont Renl-équivalent par une bijection f, alors S1i’ et S2j’ le sont aussi pour tout coloriage i’ de S1 et j’ de S2, j’ correspondant à i’ à travers la bijection f. Ainsi, les répartitions des nombres d’enlacement et leur nombre de chaîne respectif seront égaux deux à deux. Il suffit de constater que nous passons d’un coloriage à un autre en inversant un ou plusieurs ronds et de rendre ce fait par un signe négatif attribué à la lettre du rond qui change ainsi d’orientation. Par exemple, notons : enl (Xi’ , Yi’) = enl (– Xi, Yi). Or le nombre d’enlacement respecte algébriquement ce signe négatif, permettant d’écrire : enl (– Xi , Yi) = – enl (Xi, Yi) Ainsi, dans ces conditions, nous pouvons noter les nombres d’enlacements les uns par rapports aux autres, comme par exemple : enl (Xi’ , Yi’) = – (XiYi). Dans le cas que nous étudions, les différents coloriages donnent les permutations de signes suivantes. ST + TJ + JS = – 3 = Sø – ST + TJ – JS = + 1 = S{S} – ST – TJ + JS = + 1 = S{T} ST – TJ – JS = + 1 = S{J} et d’ajouter que ces permutations sont respectées par la correspondance f, car : f (– Xi) = (– f (Xi)). Étant donné le résultat énoncé plus haut et la répartition des nombres de chaîne qui apparaît au cours de ces changements d’orientation, nous pouvons parler maintenant d’une équivalence entre les chaînes orientées seulement par la torsion, présentant la même répartition des nombres de chaîne au travers des diverses orientations respectives de ses composants. Elles donnent lieu à des chaînes colorées qui présenteront alors les mêmes répartitions des nombres d’enlacement dans le cas de chaque orientation respective. a2 - Des chaînes non orientées par la caractéristique Pour une chaîne donnée non orientée par la caractéristique, nous appelons répartition des nombres de chaîne, la distribution de ses nombres de chaîne répartis d’entre les orientations par des coloriages. Pour en avoir une figure, il suffit de se reporter à notre exemple. Il s’agit de la répartition des nombres définis pour chaque coloriage par l’expression :
Définissons une relation entre les chaînes non orientées par la caractéristique. RS-équivalence Deux chaînes de présentation respective S1 et S2 non colorées seront dites RS-équivalentes, si et seulement s’il existe une bijection g entre les orientations possibles de leurs composants respectifs telle que pour toute orientation i de S1 et, par conséquent, g (i) de S2, l’égalité : Si (S1) = Sg(i) (S1) soit vérifiée. Dans ce cas, elles sont dites avoir la même répartition de leur nombre de chaîne. Cette relation est une relation d’équivalence entre les chaînes orientées par les signes de torsion.
fig. 19 Passage d’une relation à l’autre Deux chaînes de schémas plats S1i et S2j orientées par la caractéristique et Renl-équivalentes, seront RS-équivalentes en tant que chaînes non orientées par la caractéristique. Ceci se déduit immédiatement du résultat énoncé plus haut à propos de différents coloriages, en tant que l’existence de la bijection g est assurée par le jeu des changements de signe au travers des changements d’orientation. Passage dans l’autre sens Deux chaînes de présentation S1 et S2 non-colorées et RS-équivalentes, seront Renl-équivalentes en tant que chaînes orientées par la caractéristique pour un quelconque couple de coloriages respectifs mis en correspondance par g. Ceci se démontre grâce au simple calcul linéaire, à partir de la répartition des changements de signe d’entre les coloriages. Nous pouvons en effet retrouver les C2n nombres d’enlacements des composants pris deux par deux. Afin d’exprimer ce résultat, nous utiliserons l’indexation des nombres de chaîne que nous avons présentée plus haut. Avec cette notation, il est facile d’écrire comment calculer le nombre d’enlacement d’un couple quelconque de composants connaissant les nombres de chaîne. Ce nombre est donné, dans le cas le plus général, par l’expression : enl (X, Y) = 1/4 [(Sø + S{X, Y}) – (S{X} + S{Y})] montrant par conséquent que la répartition des nombres de chaîne restitue bien la répartition des nombres d’enlacement. Dans notre exemple, particulier du fait de ne comporter que trois ronds, connaissant les Si nous pouvons calculer les nombres d’enlacement respectifs de deux ronds quelconques pour le coloriage initial grâce à une formule plus simple, soit : 2 XY = (Sø + S{Z}) = – (S{X}+ S{Y}) En effet, par exemple : 2 TJ = ( –3 + 1) = – (1 + 1) = –2. Cette expression vérifie la formule précédente si le lecteur tient compte de la complémentarité ensembliste entre{Z} et {X, Y} dans {X, Y, Z} et le fait que les nombres de chaîne sont égaux lorsqu’ils sont indexés par des sous-ensembles complémentaires dans l’ensemble des lettres marquant les ronds. Nous appellerons donc l’état de l’enlacement aussi bien les répartitions des nombres d’enlacement que la répartition des nombres de chaîne. a3 - De la variation de la coupure toujours D’après les résultats précédents, les répartitoires des coupures de deux schémas plats S1 et S2 sont mutuellement translatés. Avec ou sans coupure Deux chaînes non orientées par les caractéristiques dans les présentations respectives Sp et Sp’ seront RS-équivalentes si et seulement s’il existe une bijection g entre leurs coloriages telle que pour toute orientation i des ronds de Sp et par conséquent g (i) de Sp’ : kip (Sp) – kg (i) p’ (Sp’) = lpp’ où lpp’ est une constante indépendante de i. Ceci se déduit de la définition de RS, de l’expression de la coupure et de notre résultat principal : kip (Sp) = Sp (Sp) – Si (Sp) Sachant que Sp (Sp) est indépendant de l’orientation i, le nombre : kip (Sp) – kg (i) p’ (Sp’) = Sp (Sp) – Sp’ (Sp’) = lpp’ est bien constant lorsque i varie. Précisons, comme nous le proposions, la terminologie en ce qui concerne spécialement les nœuds impropres. Nous regroupons dans un nouveau tableau, affiné du précédent, les distinctions rencontrées dans ce chapitre.
Terminologie pour les chaînes et les nœuds alternables de 1, 2 et 3 ronds dans leur présentation minimale alternée. La notion de Nœud, écrite avec une majuscule, correspondant à la non-variation du nombre de la coupure a été introduite dans ce chapitre. Les nœuds propres sont des Nœuds, et nous parlons à leur propos de Nœuds propres lorsqu’ils nécessitent une coupure. Les nœuds de Lacan sont très classiquement appelés ainsi du fait de n’être constitués que d’un seul rond. Nous parlerons donc, à propos des chaînœuds rencontrées dans ce chapitre, de Nœuds impropres puisque ce sont des chaînes, au sens classique du terme, à coupures constantes. Nous reprenons maintenant le terme de Chaîne, avec une majuscule, afin de parler des chaînes qui contiennent des enlacements. Il y a donc, parmi ce que nous appelions des nœuds impropres, des Chaînes que nous disons quelconques, du fait de représenter des cas hybrides contenant des enlacements et du nœud, du fait de la nécessité de la coupure. Et il y a les Enlacements qui sont des chaînes mais aussi des non-nœuds. Nous isolerons, par la suite, des non-nœuds standard, le nœud trivial fait d’un plongement simple d’un rond parmi les nœuds de Lacan, et les répartitions d’enlacements standard parmi les Enlacements. D’autre part, nous avons rencontré de nouveaux résultats concernant les répartitions d’enlacements. Étant donné deux chaînes non orientées par la caractéristique, il suffit qu’il existe deux orientations de leurs ronds respectifs pour chacune d’elles qui rendent équivalentes leur répartition des nombres d’enlacement, en tant que chaînes orientées par les caractéristiques, pour qu’elles soient équivalentes pour tout couple d’orientations respectives de leurs composants quant à la répartition de leurs nombres d’enlacement. Leurs nombres de chaîne Si seront égaux pour chaque couple d’orientations respectives de leurs ronds. Nous pouvons parler alors de la répartition des différents nombres de chaîne d’une chaîne non orientée par la caractéristique. Cette répartition se traduit en une variation de la coupure qui devient un critère de la répartition des enlacements dans une chaîne. De ce fait, cette répartition est lisible dans les dessins, établissant ainsi la lecture des nœuds dont nous nous proposions de parler au début du chapitre précédent. e1 - Variation de la coupure et nombre d’enlacement 1. Calculez le nombre d’enlacement de deux ronds en prenant la demi-somme des caractéristiques impropres, dans le cas suivant, avec la convention :
2. Cherchez le coloriage et la coupure éventuelle pour ce même cas. 3. Remarquez que dans un cas alterné, les croisements de la partie non-nœud ont un même signe, et les croisements de la partie nœud ont l’autre signe. 4. En conséquence, le calcul est plus rapide sur la figure coloriée, comment formuler le principe de cette lecture du coloriage? 5. Étudiez les autres coupures, afin de constater que la variation de la coupure est égale à deux fois le nombre d’enlacements, rond à rond. Étudiez la variation de la coupure et le nombre d’enlacement en répétant les cinq étapes de l’exercice précédent dans les différents cas suivants :
Vérifiez, dans un cas non alterné, que la variation des coupures orientées par la caractéristique donne bien le nombre d’enlacements.
© 1999 Topologie En Extension . Tous droits de reproduction et de représentation réservés. Tous les textes, dessins et graphiques reproduits dans cet ouvrage sont protégés par des droits de propriété intellectuelle détenus par Topologie En Extension. Par conséquent, aucun de ces éléments ne peut être reproduit, modifié, transmis, rediffusé, traduit, vendu, exploité commercialement ou réutilisé de quelque manière que ce soit sans l'accord préalable écrit de Topologie En Extension. |
|||||||||||||||||||
à la torsion de la présentation p de
l’étoffe et la lettre a au coloriage i, c’est-à-dire à une orientation
éventuelle des ronds de l’objet, c’est-à-dire à la caractéristique de cette
étoffe. Dans ce rapprochement l’objet a serait plutôt couleur de vide, notre
relation principale propose une écriture homologue à celle de la structure du fantasme
dont l’expression 
a été formée par
Lacan. 
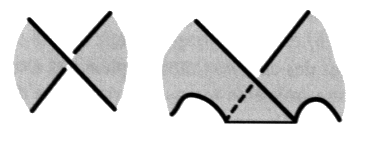
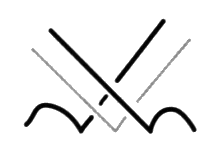
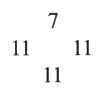
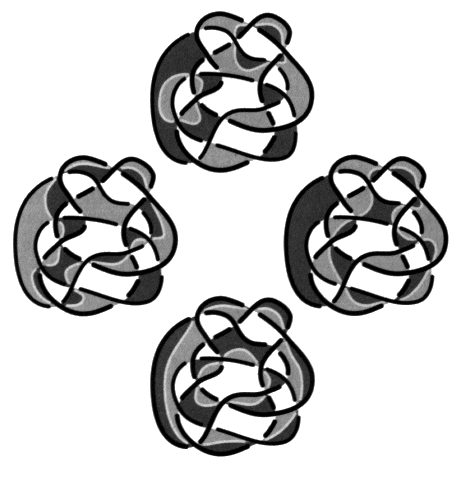
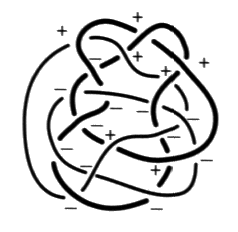
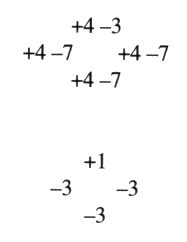
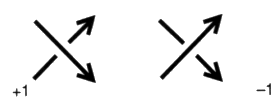
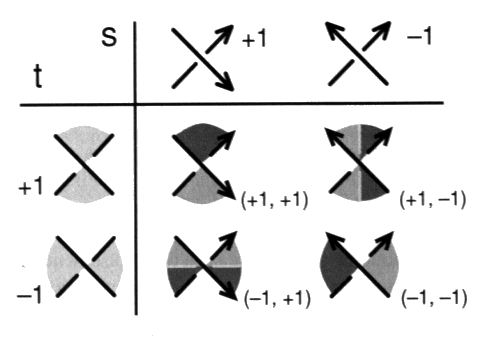
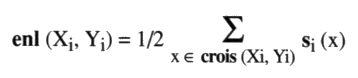
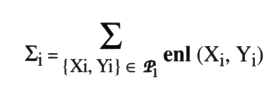
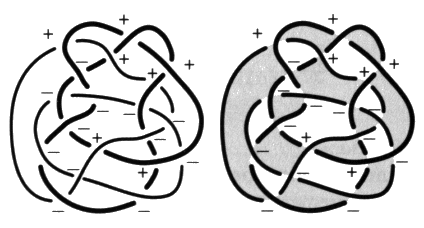
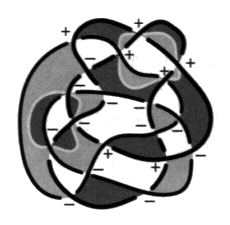
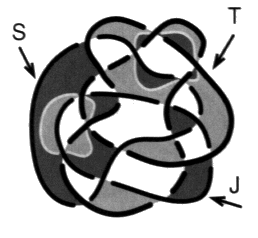
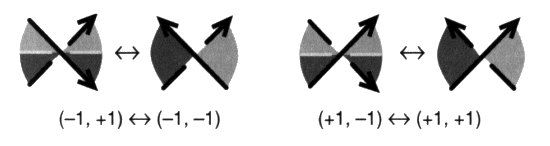
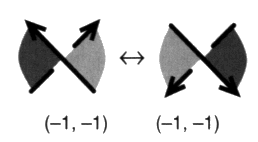
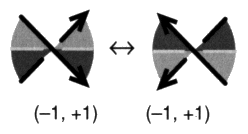
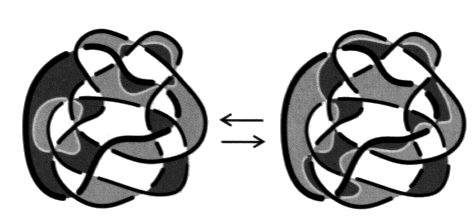
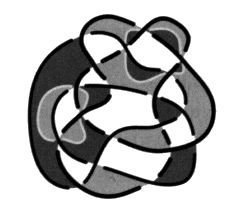
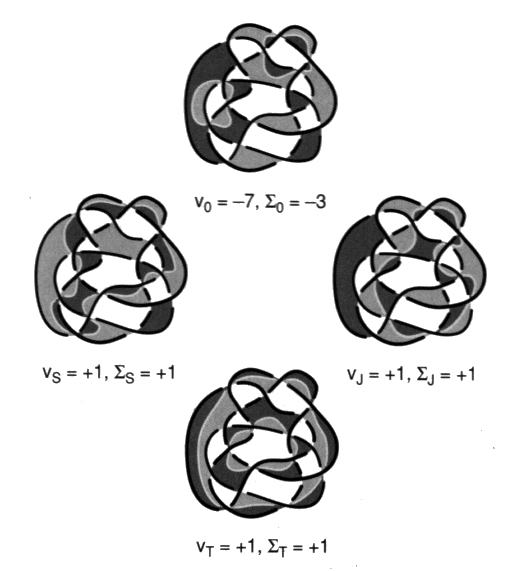
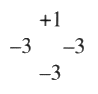
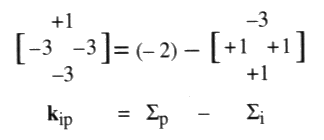
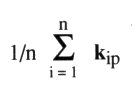
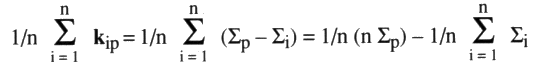
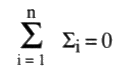
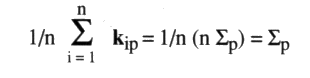
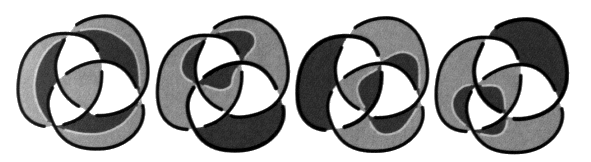
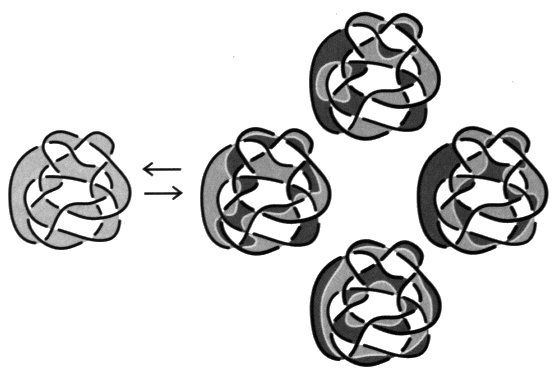
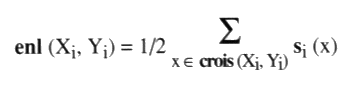
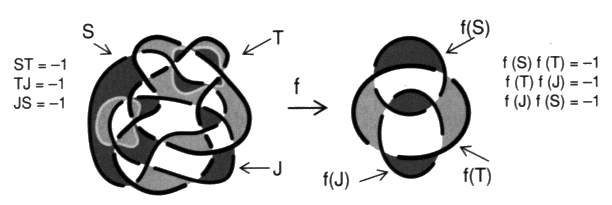
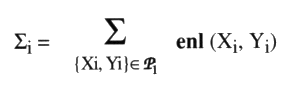
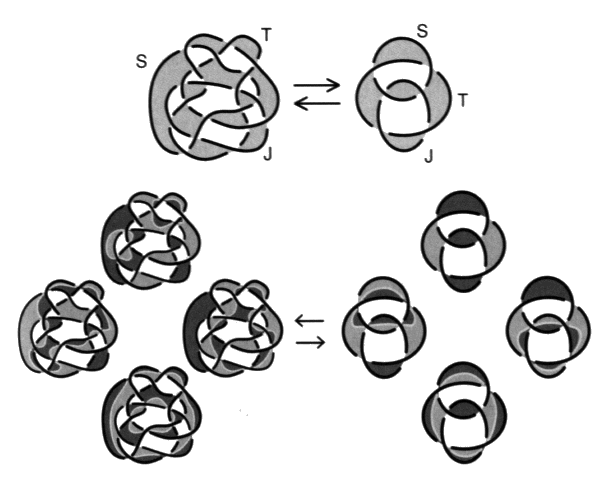
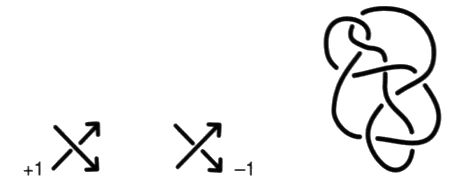Fig. a 
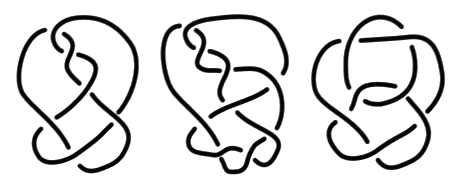Fig. b 
Fig. c