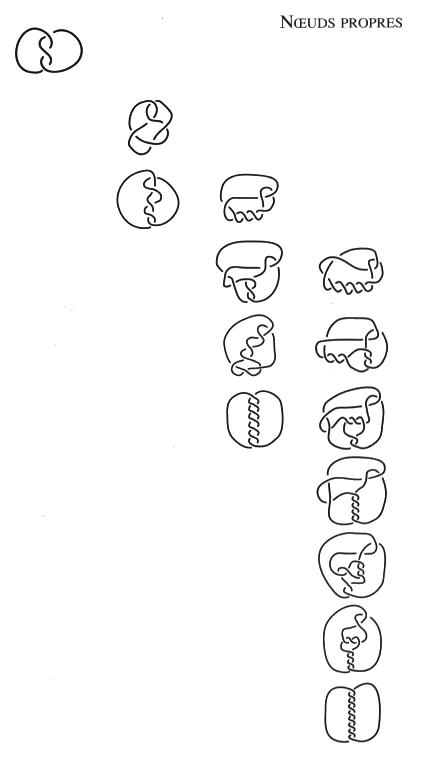
Chapitre VII Clinique des processus du nœud Aux nombres des flashes de topologie de nœuds qui ont été rapportés du séminaire de J. Lacan, il en est un qui mérite une attention particulière. Je le tiens de la publication de ce que quiconque a pu l’entendre dire dans l’année de son séminaire titrée R.S.I. [2 Sém XXII]. Ces conférences portaient sur le nœud formé par les trois consistances nécessaires à la lecture de la doctrine de Freud — le réel, le symbolique et l’imaginaire. Je ne savais pas à l’époque quelle était sa portée. Maintenant il apparaît qu’il joue pour Lacan un rôle tel qu’il s’empressa de l’effectuer afin de montrer en quoi la psychanalyse opère. C’est-à-dire de reprendre les éléments déjà présentés. En termes de schémas, avec l’involution signifiante entre le schéma R et le schéma L qui commande l’involution entre le schéma de Freud et ceux de Lacan. En termes de surfaces, avec la traduction dans le plan projectif de cette involution qui légifère entre le tore et la bande de Mœbius. Pour manifester par ces transferts un accord, sur un point déterminé, avec sa doctrine formulée maintenant en termes de nœuds. Les données de cette transformation exemplaire sont les suivantes. Une chaîne borroméenne à quatre ronds peut être réduite à une chaîne borroméenne à trois ronds en abandonnant l’un de ses ronds, celui qu’il désigne alors par les trois expressions qu’il fait ici s’équivaloir, la réalité psychique, l’Œdipe ou encore le symptôme [2 Sém XXII, leç 14.01.75]. Nous tenons ce passage du quatre au trois, où nous montrerons dans ce chapitre la fonction du trois, pour homologue à l’involution signifiante entre la perception et la conscience, dont le modèle est donné par Freud, avec le rêve de l’enfant mort qui brûle [1. a]. Lacan explique, dans cette leçon, le principe de la lecture critique qu’il fait de la doctrine de Freud. Celle-ci nécessite ce quatrième terme qui fait tenir les trois autres. Il est explicite dans la chaîne à quatre. Il veut éprouver comment ce discours peut supporter le trois où la réalité psychique de Freud est comme effacée, d’être devenue implicite dans la chaîne à trois ronds. Profitons de cette occasion pour préciser encore une fois 1 les relations qu’entretiennent les trois chapitres de l’enseignement de Lacan, en termes de graphes, en termes de surfaces et en termes de nœuds. Ils se traduisent l’un dans l’autre. Il y a donc des différences parmi les constances. La structure de l’involution signifiante est un invariant. Nous avons déjà donné la traduction des schémas en problème de surfaces2. Le lecteur peut se reporter à la présentation du mouvement de la structure à laquelle nous sommes arrivés en termes d’espace projectif troué, la bande de Mœbius, dans la conclusion de notre ouvrage précédentTrès tôt Lacan traite de l’involution signifiante — qui est au principe de la rupture de semblant, provoquant le ruissellement de petites lettres, le ravinement du signifié par cette lettre, prolongé par le ravissement qui s’en suit si le sujet compte ces éléments qui font série, sans en rater un seul — dans les termes de l’inversion du schéma R par le passage continu au schéma L où la réalité psychique de Freud chute l’espace d’un instant. Ceci se soutient de l’immersion de ces schémas sur le plan projectif. Donnons ici la présentation de ces deux états de la structure sur le plan projectif immergé 3 où nous pouvons lire que c’est bien par la rétraction de la zone  dans l’état R de cette structure que nous passons à l’état L. État sans doute instantané et refoulé du sujet qui l’éprouve, en dehors de l’analyse, dans le fonctionnement ordinaire de la structure, et le refoule au point de se croire malade quand il s’en aperçoit. Cette pulsation recouverte par toutes sortes de mystifications dans la culture qui en maintient pourtant le symbole, mais ne le produit qu’au terme des plus secrets mystères, nous l’avons construite en logique 4 à la suite de Tarski, pour démontrer, par Hans, qu’il s’agit bien de la fonction imaginaire du phallus dévoilée par Freud “comme pivot du procès symbolique” [É a 20, p. 555].Cette dynamique de la dispute, qui ne peut être évoquée que par une métaphore, va dans la culture industrielle jusqu’à se rigidifier dans l’holophrase. Cette rigidité se produit par crainte d’une forfaiture, faute d’une réflexion éthique conséquente. à l’inverse la contestation des abus est abandonnée aux démagogues les plus bêtes. Alors que les canailles prétendent justifier ces abus par la nécessité signifiante de cette structure méconnue, mais ils ne l’expliquent jamais. Reprenons la rupture de semblant, en termes de nœuds, entre la chaîne à quatre et la chaîne à trois [2 Sém XXII, leç 14.01.75]. Nous le mettons en regard de la formulation dont nous venons de faire état dans les termes d’une surface immergée. Les figures se correspondent terme à terme dans cette traduction.
La même pulsation de la structure se produit entre ces deux états de la chaîne. Mais ici, dans cette version nodale, nous verrons que c’est un des termes de la transformation qui agit en elle. Cela se passe comme nous le disions en commençant, à propos du rêve du père qui voit son enfant mort brûler en s’adressant à lui, alors que le cadavre du petit garçon a pris feu, de manière effectivement vraie, dans la pièce voisine. Le caractère plus approprié du matériel de cette formalisation, fournit une première raison de cette nouvelle traduction. Pour préciser la seconde raison de cette traduction, dans les coordonnées de la version précédente, nous pouvons nous rappeler quelle suite donne Lacan à la question préalable qu’il serait souhaitable de se poser, à l’orée de tout traitement possible de la causalité psychique, la psy-chose. En effet, sa lecture conduit Lacan à étaler les termes du délire du président Schreber sur un plan projectif troué trois fois. Or, le dysfonctionnement de la structure qui fait obstacle pour le sujet de la psychose est formulé depuis Freud, tel que Lacan le souligne, par une forclusion, comme un trou dans l’Autre, notre structure, où le signifiant n’est plus accueilli, ce qui veut dire que la signifiance, notre pulsation de structure, n’a plus lieu. Forclos est un terme de grammaire et de droit, il veut dire caduc, obsolète. Le sujet se croit être “au-dessus de ça”, c’est “bon pour les autres”, primitifs, sauvages, anciens, étrangers, barbares, provinciaux… Certains traduisent en acte cette forclusion par un “c’est dépassé”, et il n’est plus question d’y revenir. Ils réalisent la formule d’un “Je n’en veux rien savoir” en employant par exemple l’interjection “N’importe quoi!”. Ce défaut de la fonction de l’invocation de la parole, en un lieu du discours — cette parole ne raisonne plus du dire — ce dire le sujet ne l’entend plus, il ne veut plus l’entendre en ce lieu, au-delà du fait qu’il l’oublie usuellement. Il exclut cette fonction, certes impérative, du signifiant, qui s’en trouve de ce fait renforcée. L’incrédulité préside à la croyance délirante. Cette fonction est reconnue ordinairement par le sujet sans la penser. Frôlant l’impossible qui lui donne sa valeur éprouvée, si elle est rencontrée à l’occasion, elle fait événement. Faute de pouvoir à son propos métaphoriser l’événement, par la pulsation assumée de la structure — il ne s’agit pas de conscience mais de reconnaissance — le sujet va l’éprouver dans sa passion, dans son délire, en un ruissellement en acte sans résolution. Car il faut que ça passe, coûte que coûte, contrairement à ce que croit la pensée évolutionniste, et ne pouvant emprunter la voie de l’écrit dans la parole, le ravinement des petites lettres, ça passera par l’épreuve, moins masquée au sujet lui-même, de la structure en question. Il s’éprouve xénopathe. Lacan rend cette situation par des trous dans la structure. 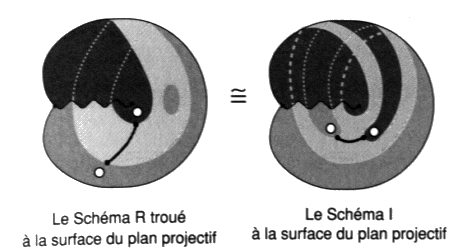 Fig. 3 Fig. 3
C’est donc comme un trou (a, a’) dans la zone Â, qui lui interdit de se fermer pour s’ouvrir, corrélé aux deux trous P 0 et F0 respectivement dans les zones S et I, que Lacan, en 1956, thématise ce défaut. Posant la question de la conception que nous pouvons nous en faire comme “simple effet dans l’imaginaire” ou comme un renvoi au narcissisme (É a 20, p. 571]. Ce trou empêche l’effacement momentané, par rétraction, de la zone Â, la chute de S.Montrons que cette situation est bien celle du schéma I, puisque celui-ci s’obtient de la déformation, Lacan parle de caricature [É a 20, pp. 563-575], du schéma R ainsi troué. Nous établissons cette correspondance au travers de la série de figures placées hors texte dans les deux pages suivantes. Nous pouvons alors nous poser la question. Ce que nous appellerons avec Lacan, la subjectivité scientifique, change-t-elle quelque chose à ce à quoi la psychanalyse se doit de répondre? Ce n’est pas la subjectivité du savant. En effet, Lacan définit, à la fin de ses propos préalables, cette subjectivité scientifique, “celle que le savant à l’œuvre dans la science, partage avec l’homme de la civilisation qui la supporte”. Il s’agit bien plutôt de l’attitude déjà notée par G. Bachelard dans son nouvel esprit scientifique lorsqu’il fait la remarque qu’un savant atomiste peut parfaitement concilier, dans sa division subjective, les croyances animistes, par exemple, ou religieuses de sa culture maternelle avec ses théories scientifiques. Où l’on voit l’état de dégradation mentale atteint par certains savants aujourd’hui, qui se croient obligés de rejeter leur culture au nom du manifeste du cercle de Vienne. On sait que cette pétition de principe prétend rejeter la psychanalyse et n’accepte de reconnaître que le comportementalisme (behaviourisme). Il n’est pas étonnant alors qu’autisme soit en augmentation (F. Dolto) et que le politique se dégrade jusqu’au juridisme et à l’intégrisme. Caricature de la réalité selon le président Schreber
Lacan cerne alors cette position subjective par les trois coordonnées d’un “discours sur la liberté”, d’un “concept du réel” et d’une “croyance dans le père Noël” où nous reconnaissons l’interlocuteur, lors du débat sur le vide, de B. Pascal. Ce “discours sur la liberté” est qualifié de délirant, nous en avons le témoignage quotidien dans ce qui se publie et dans ce qui se diffuse par des gens qui passent pour sérieux. Il n’est pas étonnant, dans ce contexte, que les bateleurs d’estrades tentent de rivaliser de démagogie avec tous ceux qui touchent au politique. Le “concept du réel” est un alibi dont les savants sont les complices, otages d’un pacte qui se voue à méconnaître la question du sujet, du sujet de la science entendons-nous bien, jusque dans le négoce. Il est déjà arrivé que l’on vende du sang contaminé par un virus sous prétexte de bonne gestion. La psychose sociale, alliée à la croyance dans le père Noël, instaurée par Pascal donc et qui se prolonge avec Newton, Marx, Einstein, Lénine jusqu’à Freud, Lacan et beaucoup d’autres, fournit les coordonnées de ce à quoi seul le discours de l’analyse peut répondre lorsque la psychanalyse a rendu les armes devant le malaise dans la civilisation. Il ne s’agit pas de faire la psychologie du savant. Nous devons accueillir ce sujet responsable de l’erreur de la manipulation laborantine, sans tomber dans cette goujaterie, comme en ce qui concerne l’artiste. Car ici aussi le psychanalyste n’a qu’à suivre. Un auteur comme K. Popper situe ainsi très bien, en dehors de ses préoccupations, la question du désir qui anime le chercheur lorsqu’il se voue à un domaine d’investigation. “Il se trouve que les arguments présentés dans cet ouvrage sont tout à fait indépendants de ce problème.” Mais il ne commet qu’une erreur, celle de rejeter cette question de la logique et de la ranger comme relevant de la psychologie, en se référent à Einstein. “Cependant, j’estime à ce propos que la méthode logique ne se confond en rien avec le fait d’avoir de nouvelles idées, ou de reconstruire logiquement ce processus. Je puis exprimer ma conception en disant que chaque découverte contient un « élément irrationnel » ou « une intuition créatrice », au sens bergsonien de ces termes. C’est ainsi qu’Einstein parle de la « recherche de ces lois hautement universelles grâce auxquelles il est possible d’obtenir par pure déduction une image du monde. Il n’y pas de voie logique », dit-il, « qui conduise à ces lois. On ne peut les atteindre que par une intuition fondée sur une sorte d’amour intellectuel (“Einfühlung”) des objets d’expérience »” [56, p. 28]. Or nous avons montré après Lacan et après Spinoza que cet amor intellectualis de l’objet relève d’une logique classique modifiée en une topologie du sujet. Du même coup, Popper passe à côté de Freud, à qui il reproche le vérificationnisme qu’il croit déceler dans son approche, ce dont il a tort, car Freud réfute constamment sa doctrine qui se révèle toujours irréfutable, et relevant par conséquent de la topologie du sujet. Ainsi Popper rate la place de la psychanalyse dont il donne pourtant ici les coordonnées. La psychanalyse se trouve par là même située, pour nous, dans ces catégories, par rapport à la recherche scientifique. Ce n’est pas où il croit devoir la placer. Elle n’est pas une discipline expérimentale, où règne la concurrence des théories qui se falsifient entre elles (version poppérienne de la science). La psychanalyse relève d’une logique non valide mais irréfutable, notre topologie. C’est dire qu’elle n’est pas une science, mais qu’elle n’est pas non plus, ni une métaphysique, ni une idéologie. C’est là que la pensée politique de Popper et la libre entreprise échouent dans la cité, complices du crime de la bonne gestion parce qu’elle croit réguler, comme disent ces gens-là, la question du sujet par la concurrence au lieu de la raison. Une autre politique est réclamée à cet endroit, c’est dire que le problème de la vertu n’a pas été résolu par les aménageurs de conscience (managers) prétendument sans idéologie. Le débordement des techniques, issues de la science, elle-même produit du retournement de la théologie, en particulier catholique, en anthropologie, ce dont témoigne Descartes, voit croître et s’étendre, en pure méconnaissance, dans la cité et dans l’impire, la subjectivité scientifique, définie par la civilisation de l’occire. Il faut à un J.R. Oppenheimer d’avoir construit la Bombe pour commencer à s’inquiéter du désir dans la science au regard du bon sens. Cette science nouvelle, pronostiquée par Galilée, est plus subie par ses savants, et la civilisation qui les supporte, que décidée par eux. La relation des experts et des politiques se trouve ainsi ramenée à sa dimension réelle. À la suite d’une pratique de la psychanalyse, de plusieurs décennies, le constat par Lacan, des difficultés, voire des butées rencontrées dans la pratique, nous mène à considérer que le défaut aperçu dans la psychose de Schreber, est beaucoup plus fondamental pour la subjectivité scientifique, pour le sujet qui vient en analyse. Lacan va, au cours d’une intervention parlée dont il a le secret, où il midit pas tout, à la fin d’un congrès, à Deauville, dans les années soixante-dix, jusqu’à se demander si tous les gens qui viennent chez lui ne sont pas psychotiques. Ironie de psychiatre à l’adresse des intéressés. “Pourquoi viendrait-on demander à un analyste le tempérament de ses symptômes? Tout le monde en a, étant donné que tout le monde est névrosé. C’est pour ça qu’on appelle le symptôme, à l’occasion névrotique, et quand il n’est pas névrotique, les gens ont la sagesse de ne pas venir demander à un analyste de s’en occuper. Ce qui prouve quand même que ne franchisse ça, à savoir venir demander à l’analyste d’arranger ça, que ce qu’il faut bien appeler le psychotique.” J. Lacan, citation libre recueillie aux assises de Deauville, janvier 1978, ce n’est pas extrait d’un Écrit. Nous ne disons pas, comme on a voulu nous le faire dire que “dans la civilisation scientifique tout le monde est psychotique”, et nous ne l’écrivons pas. Lacan non plus, car dans ses Écrits, il emploie plus volontiers les expressions de psychose et de processus psychotique, ainsi avons nous relevé cette catégorie de la subjectivité scientifique. Pour notre part, aujourd’hui, nous nous devons d’être plus précis, en reprenant le terme de psychose sociale afin de bien indiquer ce dont il s’agit à propos de ce processus, ne voulant pas favoriser la goujaterie que nous signalions plus haut, si répandue aujourd’hui, à l’impuissance dix, nous voulons parler de moyens mentaux, depuis la disparition de Lacan. C’est que nous prenons plus volontiers nos repères cliniques et de méthodes chez R. Jakobson que chez M. Foucault5. L’étude des aphasies dû à Jakobson [47], sur la base de sa poétique, reste en matière de clinique structurale, un modèle du genre, hors les deux fondateurs de la psychanalyse. C’est autre chose que l’histoire de la folie à l’âge classique qui ne distingue même pas entre folie et causalité psychique. Pour s’y retrouver, nous conseillons au mieux de lire B. Ogilvie [54], où est mis définitivement au point ce que l’on peut attendre d’une exhaustion clinique comme Lacan l’a tentée dans sa thèse de médecine. C’est à s’apercevoir de la nécessité de la structure entre matériaux innés et acquis. Indébrouillable sans cela, mais bien sûr un lecteur moyen ne s’en aperçoit même pas. Pas avant longtemps, car il faut suivre les raisons, sans en louper une, avant que ça se boucle sur l’impossible6. Il y a un drame dans la science, dont celui qui se joue dans l’analyse est exemplaire, mais Lacan pose la question de savoir s’il relève toujours de l’Œdipe, sauf à le mettre en cause [É a 32, p. 870]. Ce qui se passe dans le discours analytique est donc exemplaire mais n’en est pas exempt. Ce lien social fait partie de la question et l’on ne répond pas bien à ne pas le mettre en cause, ou à ne mettre que de pauvres petites gens sur la sellette à des fins d’intimidation et de pouvoir, cela se voit aujourd’hui, faute d’une réponse appropriée qui mette quiconque à contribution. Disons pour commencer en quelle estime nous tenons ceux qu’il ne faudrait pas dire nos collègues, le terme ne convient pas dans ce champ, mais nos pairs. Nous nous adressons ici aux analysants de Freud et de Lacan, comme aux analysants de ceux-là. Cette communauté liée par une expérience unique dans le siècle a toujours méritée notre considération fraternelle. Mais ce constat, il ne faudrait pas le dire aux tenants lieu du psychanalyste qui restent bouche bée devant ce qu’il nous faut reconnaître dans le transfert. L’ignorance la plus crue sur le point de la reconnaissance du désir dans les détours de son acte. Il ne faudrait pas le leur dire, pour ne pas les affoler, afin qu’ils puissent continuer à croire qu’ils pratiquent une technique thérapeutique et qu’ils sont des saints, il en faut. Qu’ils peuvent faire tout de même, dira-t-on, quelque chose pour quelqu’un, ou qu’ils en ont le pouvoir, croyance qu’ils protègent, pensant par là qu’on aura recours à eux. Les plus aventureux d’entre eux croient pouvoir un jour guérir la psychose, alors qu’ils ne voient même pas que tout le monde verra qu’ils ne voient pas qu’elle se développe dans le bruit et la fureur autour d’eux. On joue sur du velours quand le massacre continue alentour, juste un peu plus loin. Le cynisme partagé se contente de réclamer et de répondre à la demande sociale, où l’on puise, chez les divers travailleurs sociaux, le modèle d’une pratique, au lieu d’en importer une autre. Certes, il faut ménager le narcissisme du groupe. Mais ce n’est pas pour qu’ils puissent continuer à s’y croire suffisants à remplir sa tâche, qui consiste à occuper cette place nécessaire du semblant pour les autres. Resterions-nous dans le champ de Freud à méconnaître que la psychanalyse existe et à faire croire qu’il ne faut que se contenter d’en maintenir le courant dans la vraie semblance. C’est ce que certains esprits habiles ont cru bon de mettre en œuvre. Ou bien il faudrait cacher à nos contemporains cette passion de l’ignorance qui les habite et dont ils ne veulent rien savoir, ce diagnostic et la façon d’y répondre. Soit prendre acte que le sujet cartésien, le sujet de la psychanalyse, est bien défini par une fétichisation de l’être. Soit aussi reconnaître, dans le passage de la clinique à la pratique de l’analyse, que s’il y a des trous de structure pour quiconque dans cette civilisation, nous quittons peut-être une simple réduction à l’Œdipe, mais les bords de ses trous sont noués. Or les bords de ces trous sont des ronds dont l’agencement nécessite une suppléance — ça, certains l’ont aperçu, mais n’en ont rien fait qu’une holophrase de plus, réservant cette suppléance à la psychose — lorsque le sujet ne parvient pas à les nouer à la manière qui le réclame, au plus pur. Lacan a répondu par des ronds, des ronds… à la question toujours préliminaire que se pose à elle-même la subjectivité scientifique dans ce contexte de psychose sociale, entendez l’économisme politique aussi bien. Et ces ronds forment un nœud. Mais c’est pour souligner la pulsation qui doit toujours être assumée en raison par chaque sujet, qui lui impose de supporter ce glissement instantané de la réalité psychique selon Freud, dite aussi Œdipe, puisqu’elle en est le principe de l’amour pour le père. C’est la structure du symptôme. Cette jouissance que trouve la vérité pour s’opposer au savoir [É a’ 13, p. 58]. Son effacement n’est que momentané, telle le phœnix elle renaît toujours de ces cendres, et même immédiatement. C’est pourquoi ce sésame de la structure ne sera jamais touristique [É a 30, p. 838]. Parlant du nœud borroméen, Lacan précise :
Il s’agit bien d’une erreur, et la dénoncer n’a rien de la recherche d’une totalité. Quant à l’absolu, il s’agit du détachement. Absolu veut dire séparé, Lacan poursuit :
En définissant la perversion en liaison avec l’amour pour le père comme jamais cela n’avait été fait auparavant. D’où nous sommes repartis avec Hans et Tarski de son ratage dans la phonction fallique.
J. Lacan [2. Le sinthome]. Nous voici avertis, ce dont nous repartons, la fonction à laquelle satisfait ce quatrième terme et sa topologie qui n’a rien d’une chaîne rompue. Seulement version vers le père, toujours ratée, mais comment? Nous montrons maintenant ce qui est raté, le ratage de l’effectivité du trois par le quatre. Mais par où il faut savoir passer. Cette transformation d’une chaîne à quatre en une chaîne à trois, puisque c’est ainsi que maintenant on le formule, telle que Lacan l’a montrée au tableau [2 Sém XXII, 14 janvier 1975], doit être précisée, pour être bien définie, comme un mouvement gordien. Il faut colorier la 4-chaînœud :
Puis effectuer le gordien sur deux croisements. Il consiste à inverser ces deux croisements, ici entre les ronds R et S, 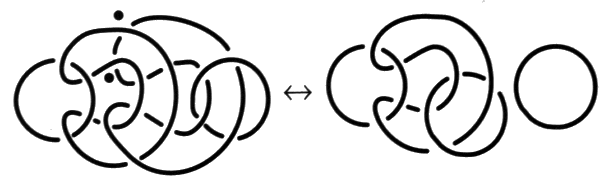 Fig. 5 Fig. 5
afin de faire glisser le rond S, sinthome, Œdipe, réalité psychique, amour vers le père, jouissance, qui ne tient plus le temps d’un instant. C’est dans le contexte de cette question que nous entendons traiter de l’objet dans la psychose, en tant que nous voulons montrer en quoi et à quel titre, le nœud de trèfle devient l’homologue du schéma I, soit le schéma R troué de trois trous :
afin de rendre compte de la psychose paranoïaque [2 Sém XXIII] dans ce chapitre de l’enseignement de Lacan. Le nœud trèfle est un nœud propre homologue à la chaînœud borroméenne modulo deux mises en continuité par des sections transverses. Notre dernier résultat concernera cette homologie indépendamment du nombre de ronds dans les objets. Montrons maintenant avec le principal résultat de cet ouvrage, le mouvement nœud, susceptible de fournir les moyens de la définition du nombre de nœud contenu dans un objet, que la 3-chaînœud borroméenne est bien le moyen de formuler implicitement la 4-chaînœud, mais du même coup elle condense aussi cette involution entre chaînes. Nous pouvons reprendre la théorie T 0 des non-nœuds en termes de nœuds, avec la théorie des chaînes intrinsèques T00 et introduire un nouveau mouvement.1. Théorie des chaînes intrinsèques et théorie du nœud En définissant un nouveau mouvement, nous l’appellerons le mouvement nœud, nous pouvons formuler un nouvel invariant en théorie classique des nœuds afin de préciser notre théorie du nœud. Celle-ci se réfère à une autre théorie des enlacements, réductibles aux non-nœuds où le mouvement nœud a été substitué aux gordiens et aux homotopies, nous appellerons cette nouvelle théorie T 00, la théorie des chaînes intrinsèques7.Par rapport à cette théorie des chaînes intrinsèques, nous construirons d’abord une théorie des nœuds afin de définir le nombre de nœud, puis nous réduirons celle-ci à une théorie du nœud. Commençons par définir ce nouveau mouvement N 3 qui s’effectue sur les triskels alternés :
Ce mouvement équivaut à ajouter une chaînœud borroméenne à un triskel alterné.
Cette présentation du mouvement nœud justifie que nous l’appelions mouvement chaînœud borroméenne ou mouvement borroméen. Le rôle qu’il va jouer en théorie du nœud établit la fonction de structure qui lui est accordée dans le champ freudien par Lacan. Cette butée nécessaire, jamais produite auparavant, permet de lire enfin comment c’est à recourir à la chaînœud borroméenne que nous pouvons opérer sur le trèfle qui est le premier nœud premier 8.
Nous allons préciser comment nous en servir dans le cas général. Ce mouvement nœud est un composé de mouvements élémentaires dans notre précédente théorie des enlacements. La série qui le représente contient toujours un mouvement T 3 et un gordien, parmi des mailles.De cette manière : 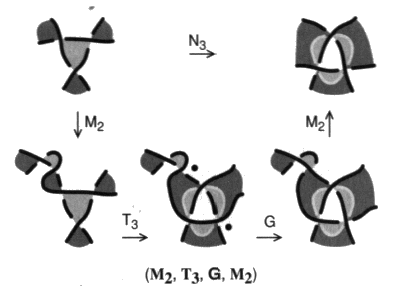 Fig. 10 Fig. 10
Soit de celle-ci : 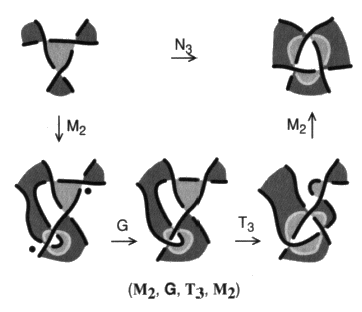 Fig. 11 Fig. 11
Nous chiffrons ces nouveaux mouvements de façon à ce que leur nombre, a, puisse être exprimé dans le nombre de nouage par la formule 3a = 2g + t. Il faut remarquer que si un mouvement nœud se substitue à un gordien spécifique, accompagné d’un mouvement T 3, n’importe quel gordien n’est pas nécessairement susceptible d’être rendu par un seul mouvement nœud, mais il est certainement rendu par plusieurs mouvements comme nous allons le montrer maintenant.a2 - De la théorie des nœuds extrinsèques à la théorie des chaînes intrinsèques Afin d’écrire une théorie T N des nœuds et de construire le nombre de nœud, pour un nœud ou une chaîne quelconque, nous procéderons au dénouage (effacement) de cet objet dans une théorie T00 des chaînes intrinsèques, où les mouvements nœuds positifs remplacent les mouvements gordiens et les homotopies de la théorie des enlacements précédente, et où nous maintenons le recours aux mouvements de Reidemeister.Nous définissons alors, grâce à ces changements de présentations, une relation R N (S1, S2), sur l’ensemble des présentations de nœuds ou de chaînes.Soit : R N (S1, S2) Û $ $ ( $ ( S1) = S2)Cette relation est une relation d’équivalence. Nous la noterons parfois S 1 »N S2.
Nous appellerons chaînes les classes d’équivalence définies par cette relation. Ces classes de présentations constituent les objets de la théorie T 00.Cette théorie T 00 des chaînes intrinsèques est la théorie de ces classes d’équivalences et il est aisé de montrer par un calcul sur les signes de croisement d’une orientation quelconque (voir Fig. 27), lorsqu’il s’agit de croisements impropres, que ces mouvements respectent la répartition des nombres de chaînes, et par conséquent la relation RS.Les objets identiques de cette théorie ont mêmes enlacements Pour deux présentations de chaînes ou de nœuds S 1 et S2 :RN (S1, S2) Þ RS (S1, S2) Nous donnons maintenant la preuve de l’implication réciproque selon laquelle deux chaînes présentant la même répartition de leurs nombres de chaînes respectifs, RS -équivalents, seraient identiques dans la théorie des chaînes. Cela revient à se poser la question de savoir si pour deux chaînes S1 et S2, RS -équivalentes, il existe toujours entre elles une série $ de mouvements de notre nouvelle théorie des chaînes telle que : S2 = $ ( S1) Répondre affirmativement à cette question, c’est démontrer le théorème suivant. Deux non-nœuds équivalents sont deux objets identiques Si deux chaînes S1 et S2 sont RS -équivalentes, alors elles sont RN-équivalentes : RS (S1, S2) Þ RN (S1, S2) Nous savons déjà, à propos de la relation R0 en place de RN, pour l’avoir rencontré avec l’usage de la composition # dans notre théorie des enlacements, en termes de gordiens et d’homotopies, que la démonstration de ce théorème nécessite de démontrer deux choses que nous regroupons ici en un seul énoncé. Les chaînœuds et les nœuds propres sont sans enlacement Une chaînœud (respectivement un nœud propre) est toujours réductible, par une série de mouvements de la théorie T00 des chaînes intrinsèques, à une chaîne triviale (respectivement un rond trivial). Donnons une démonstration de ce théorème dont il est remarquable qu’il suffise qu’il porte sur les chaînœuds et les nœuds propres. Grâce aux mouvements M2, T3 et N3, nous pouvons extraire un quelconque rond d’une chaînœud. Le mouvement N3 permet de passer les obstacles représentés par les triskels alternés. En effectuant ces mêmes types de mouvements, nous pouvons extraire un par un chacun des ronds d’une chaînœud puisqu’elle ne contient pas d’enlacement. Le théorème est démontré du fait qu’aux mailles et aux triskels non alternés s’appliquent des mouvements M2 et T3, et qu’aux triskels alternés nous pouvons recourir au mouvement N3. Il n’y a pas de maille alternée sans une autre maille alternée de torsion inverse qui la compense, et nous ne rencontrons pas d’autre cas de figure. Montrons cela sur un exemple; nous reprenons la partie du montage K2–1 # S2 déjà rencontré au chapitre IV.
Dans cette théorie des chaînes, chiffrons l’ensemble de nos mouvements nœuds disposés dans le tableau 3, ce chiffrage élémentaire se trouve résumé dans le tableau 4 en regard du précédent. Étant donné un changement de présentation $ défini par la série (X 1… Xn) avec Xi appartenant à l’ensemble de nos mouvements, nous pouvons définir l’ensemble s des chiffres de la série :s = {b, b*, t, a} Il est alors facile de calculer la proposition suivante. Relation entre les moyennes des nombres de coupure Si deux chaînes S1 et S2 sont liées par la série des mouvements $ de chiffre s telles que : $ (S1) = S2, alors les moyennes des nombres de coupure de ces deux chaînes vérifient : S (S2) = b + t + 3a + S (S1) S*(S2) = – b* – t – 3a + S*(S1) si s = {b, b*, t, a}. Et de se saisir de la nouvelle définition des nombres de nouage. Définition Nous appellerons nombres de nouage duaux l’un de l’autre les deux expressions : Ns = b + t + 3a N*s = – b* – t – 3a Ces définitions étant formulées, nous pouvons parler maintenant de la théorie TN des nœuds. Notre théorie TN des nœuds est alors extrinsèque à cette théorie T00 des chaînes. Ses mouvements sont les mouvements de Reidemeister, de la théorie classique des nœuds. Ses objets sont les classes d’équivalence produites par ces mouvements. Nous retrouvons donc la théorie TC classique des nœuds où nous définissons par un calcul un nouvel invariant grâce à ce rapprochement avec la théorie T00 des chaînes intrinsèques. Le calcul consiste à dénouer les présentations de manière intrinsèque à la théorie T00 des chaînes afin d’obtenir une analyse de leur nombre de nouage, dont nous ne retenons que le nombre de mouvements nœud noté a, afin de chiffrer le nombre de nœud. Ce nombre est invariant pour les isotopies d’ambiance (les mouvements de Reidemeister), puisqu’il ne dépend ni de B1, ni de M2, ni de T3, ces mouvements ne faisant varier que le nombre de nouage mais pas le nombre de nœud. Nous commençons par déterminer, dans un nœud ou une chaîne quelconque S, la répartition des nombres de chaîne Si grâce aux nombres d’enlacement aisés à calculer par les coloriages. Les nœuds propres ont un nombre de chaîne nul, le non-nœud S0 qu’ils contiennent est trivial. Dans le cas des chaînes de deux et trois ronds, ceci nous permet de déterminer quel est le non-nœud S0 contenu dans la chaîne. Dans le cas des chaînes de quatre ronds et plus, la répartition des nombres de chaîne Si nous permet de déterminer la présentation minimale alternée S0 contenue dans la chaîne. Cette présentation minimale alternée peut être un non-nœud, ou bien une chaîne présentant une coupure comme nous l’expliquions au chapitre cinq. Le nombre de nœud sera déterminé par rapport au cas exemplaire choisi comme représentant l’état d’enlacement. S’il existe différentes séries de mouvements $ qui transforment S0 en S, ce que nous formalisons par l’expression :
qui dit que la présentation S représente le mouvement $ pour la présentation S0. Mouvement dont les nombres de nouage duaux sont exprimés dans cette nouvelle théorie des chaînes intrinsèques par : Ns = bs + ts + 3as N*s = – b*s – ts – 3as Définition Nous appellerons le nombre de nœud d’une présentation donnée le nombre minimum, noté a, des nombres de mouvements nœuds obtenu pour toutes les séries $ qui mènent de la répartition S0 des enlacements contenue dans cette présentation, à cette présentation S elle-même : a = min. as s tel que : $ (S0) = S avec Ns = bs + ts + 3as et N*s = – b*s – t*s – 3as Le lecteur peut vérifier que ce nombre est invariant pour les isotopies d’ambiance, puisqu’il ne dépend pas des mouvements B1 et T3 et qu’il est indifférent aux mouvements M2. Donnons un exemple d’un tel calcul dans un cas non alterné :
Le calcul de la répartition des nombres de chaînes Si pour les diverses orientations donne les résultats suivants9 : S{Ø}= +1, S{S}= –3, S{T}= +1, S{J }= +1 où nous reconnaissons la répartition de la première chaîne olympique de torsion négative déterminant ainsi S0 :
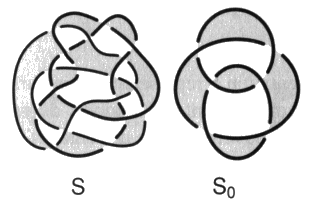 Fig. 15 Fig. 15
Il faut déterminer la série $ des mouvements qui transforme S0 en S. Pour cela nous dénouons S en S0 par une série de mouvements en passant à la présentation duale lorsque ceci est nécessaire à l’effectuation de mouvements N3.  Fig. 16 Fig. 16
Nous venons de dénouer S en S0 par une série de mouvements; notons-la $–1. Il est facile de déterminer la série $ des mouvements qui transforme S0 en S. Il suffit de reproduire cette série de mouvements rétroactivement, en prenant soin de passer au dual, lorsqu’il est nécessaire d’effectuer un mouvement N3. Nous pouvons ainsi vérifier que le nombre de nœud est ici certainement inférieur ou égal à deux, soit a £ 2. Il y a toujours la même indécision relative à son caractère minimum.
Comme nous calculons toujours avec le nombre de nouage le nombre de nouage dual, ces différents passages à la présentation duale sont faciles à contrôler par le calcul, ils ne font que transposer entre eux ces deux nombres. La seule question qui reste en suspens est de s’assurer qu’il s’agit du nombre minimum de mouvements nœuds, ce qui n’est pas décidé, mais qui n’empêche pas le nombre de nœud d’exister. a4 - En jeu de ce nouvel invariant Le calcul du nombre de nœud par le dessin dépend de cette indécision, et on peut se proposer en mathématiques de rechercher un polynôme de nœud, à la manière du calcul d’entrelacs (Skein calculus) dont le degré d’un facteur pourrait produire ce nombre à partir d’une quelconque présentation. Sinon, la preuve qu’un tel polynôme est impossible à construire, est aussi un résultat qui présente un grand intérêt afin de fournir, par une raison contraire, quelques éclaircissements dans ce domaine nodal. À l’occasion du calcul du nombre de nœud, nous voyons se révéler l’intérêt de la dualité pour le choix de la présentation préférable des cas alternés, et par suite des cas non alternés. Ainsi le fait que S représente un mouvement $ pour S 0, produit le nombre de nœud a, ce que nous rendons par l’expression :® S0 — — $ a Mais il est trivial que cet usage du nombre de nœud peut se généraliser à n’importe quel couple de présentations S 1 et S2 qui appartienne à la même chaîne intrinsèque pour la théorie T00 des chaînes intrinsèques. Une présentation S1 représentant une série de mouvements $ pour une autre présentation S2 produit un nombre de nœud a :1 ® S2 — — $ a Si a = 0, nous dirons très classiquement que S1 et S2 sont deux présentations du même objet dans la théorie des nœuds Tc. Si nous nous référons à une théorie des chaînes qui consiste à effectuer des mouvements nœuds positifs, chiffrés dans le tableau 4 (voir plus haut), et leurs inverses, chiffrés négativement, nous pouvons calculer des nombres de nœud relatifs, mais la condition qui impose de choisir la série dont le nombre de nœud est minimum, produit un quotient brutal modulo deux de ce nombre de nœud. Le nombre de nœud se réduit à 0 ou 1. Dans la théorie du nœud qui s’y rapporte, il n’y a, dans un nœud propre ou une chaîne quelconque, qu’un nœud ou pas de nœud. Dans cette théorie, il n’y a qu’un nœud. 3 par G2 et N3Pour conclure ce paragraphe consacré aux définitions, nous renouons avec l’investigation mathématique récente de la théorie classique des nœuds en apportant une précision dans l’analyse du troisième mouvement de Reidemeister. En effet, s’il est pratiqué sur un triskel fait de trois éléments de cordes distinctes, celui-ci se décompose en une série contenant un mouvement gordien de la théorie des enlacements et un mouvement chaînœud borroméenne, dans la théorie des chaînes présentée plus haut.  Fig. 18 Fig. 18
Nous proposons ce résultat à la réflexion mathématicienne, en regard du traitement qu’elle développe déjà du mouvement T3 en termes d’algèbre des solutions des équations dues à Yang-Baxter [18. c]. a7 - Le Trois est la raison du rapport de trois à quatre ronds Il nous suffira alors, pour notre part, de montrer comment la réduction de la 4-chaîne à la chaîne à trois, déjà réalisée dans ce qui précède par un mouvement gordien, se produit aussi grâce à un mouvement nœud. Nous choisissons un triskel dans une présentation de la chaîne à quatre et nous effectuons le mouvement nœud.
De ce fait nous pouvons pratiquer un mouvement M 2 dans ce dessin. Il suffirait de faire deux mouvements T3 pour dégager cette maille, nous ne le ferons pas, mais le lecteur peut le vérifier.
Le quatrième rond se détache par une série de T 3 et il ne reste qu’une 3-chaîne qui a ainsi été obtenue à partir de la 4-chaîne, du fait de l’action de la 3-chaîne à travers le mouvement nœud.
Le lecteur remarquera que nous avons choisi des présentations différentes de la quatre chaîne pour montrer comment la transformer en trois chaîne selon l’emploi du mouvement gordien ou l’usage du mouvement nœud; mais ceci n’a rien de nécessaire. 2. Différenciation de trois types de mouvements nœuds Nous pouvons maintenant apporter plus de précision dans notre analyse du nœud en filtrant la multiplicité de nos objets aux travers des trois types distincts de mouvements nœuds. Nous les définissons maintenant avec leurs objets prototypiques. Le mouvement nœud que nous venons de construire afin de définir le nombre de nœud, peut être différencié en fonction du nombre de ronds, distincts entre eux, qui sont mis à contribution dans son effectuation. Nous appellerons mouvement nœud impropre, noté Ni, le mouvement nœud lorsqu’il est effectué sur un triskel composé de trois éléments de ficelle appartenant à trois ronds différents.
Ce type de mouvement ne présente que des croisements impropres et supprime donc les chaînœuds borroméennes de trois ronds, qu’elles soient borroméennes ou bien borroméennes généralisées :
C’est l’entrée dans la subjectivité scientifique par l’absence de métaphore où se situe le délire paranoïaque. Nous appellerons mouvement nœud hybride, noté Nh, le mouvement nœud lorsque le triskel est composé de trois éléments de ficelles appartenant à deux ronds différents.
Ce type de mouvement présente deux croisements impropres et un croisement propre. Il supprime les chaînœuds généralisées de deux et trois ronds. 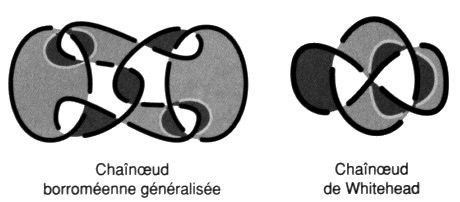 Fig. 25 Fig. 25
Les chaînœuds généralisées de trois ronds sont une modalité du quatre parmi les objets faits de trois ronds. C’est dans l’effectivité de notre théorie des objets faits de un à trois ronds, la trace ou le reste du quatre, dit de la réalité, de l’Œdipe, du sinthome ou encore de l’amour pour le père, qui permet dans l’effectivité de situer l’acte ou l’événement entre réalité et effectivité. Pour les mêmes raisons, puisqu’elles sont aussi obtenues par une section transverse, les chaînœuds de Whitehead faites de deux ronds sont une modalité du trois parmi les objets faits de deux ronds. Nous appellerons mouvement nœud propre, noté Np, le mouvement nœud lorsque le triskel est composé de trois éléments de ficelle appartenant à un même rond.
Ses croisements sont tous les trois des croisements propres. Il supprime les nœuds propres :
C’est le renoncement au délire. Le délire oublie, de manière plus ou moins partielle, la partie non-nœud des chaînœuds. a1 - Le treillis des théories du nœud Nous pouvons ainsi définir huit théories différentes qui vont nous permettre d’analyser assez finement l’espace nodal. Munis de ces définitions, nous adoptons le principe de ne recourir à ces différents mouvements que d’une façon différenciée. Les huit théories se distinguent selon que nous n’employons qu’un d’entre ces mouvements, ou bien deux ou les trois comme nous le faisions dans la théorie des chaînes intrinsèques. Chaque théorie aura ses propres théorèmes.
L’ensemble nous permettra d’envisager la façon de supprimer les enlacements, afin de n’obtenir que des théories de nœuds.
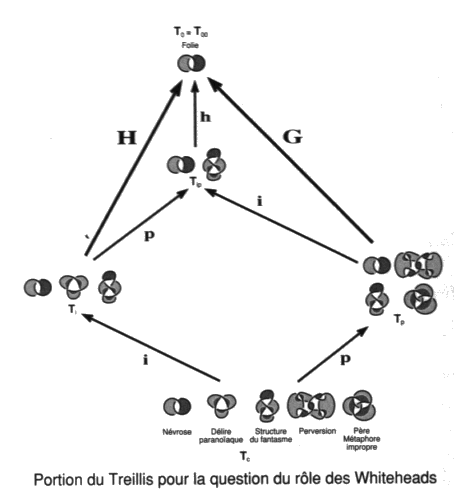
Nous n’entreprendrons cette analyse que dans les ouvrages 10 qui suivront celui-ci. La suppression des enlacements nous permettra de formuler la pratique de l’analyse en tant que refus du tore névrotique et par conséquent de la folie.En attendant d’entreprendre ces études distinctes et leur rassemblement en cette structure, le treillis de ces différentes théories nous servira pour diffracter en raison les structures freudiennes de la clinique de la psychanalyse. a2 - Précision dans le débat entre Lacan et Soury Nous disposons maintenant de l’opérateur qui supprime les complications introduites par la chaîne de Whitehead et le nœud borroméen généralisé. Complications invisibles à partir des théories à gordiens propres ou impropres près qui distinguent les avancées respectives de Lacan et de Soury. C’est le mouvement nœud hybride. Si nous reprenons le graphique que nous utilisions alors, au chapitre VI, pour les présenter, nous pouvons l’indexer par les trois types du mouvement nœud qui se trouvent ainsi disposés au regard des mouvements gordiens propres et impropres.
Portion du Treillis pour situer Lacan-Soury-Vappereau Dans nos théories de un à trois ronds, le borroméen généralisé :
représente le quatre dans le trois, soit le sinthome S. Ceci s’éclaire du fait de l’étude des sections transverses qui reste à développer. Il y a quelque chose du quatre et donc du deux dans ce trois qui est différent du trois du nœud borroméen.Par conséquent, le mouvement hybride sera plus précisément, dans ce contexte des objets faits de un à trois ronds, l’opérateur de l’involution entre le quatre et le trois. Première question mise à jour par notre présentation Une première question s’impose alors. Il s’agit de savoir ce qu’il en est des permutations entre ces types de mouvements nœuds. Autrement dit, est-ce que le diagramme suivant est commutatif?
La réponse à cette question est facile à apporter. Seules les chaînes du type Whitehead et borroméennes généralisées font problèmes. Ces chaînes se décomposent différemment au sens où les borroméens généralisés se défont aussi bien par des mouvements hybrides et par des mouvements impropres, ce qui n’est pas le cas des chaînes du type de la chaîne de Whitehead, qui ne sont trivialisées que par le mouvement hybride. Nous pouvons maintenant présenter le problème de la clinique de la psychanalyse et les structures freudiennes. Nous ajouterons ensuite une dernière définition topologique, celle de l’homologie, afin de donner sa formulation achevée au dialogue établit entre Lacan et Soury. Ce débat nous réservera encore quelques surprises du fait que Soury s’intéressait sans doute plus que l’assistance d’alors ne le soupçonnait à une clinique freudienne en terme de névrose et de perversion. Lacan étant seul à porter le fer sur le front de la psychose. Il s’agit, avec cette homologie, d’une relation d’équivalence définie entre des objets qui peuvent présenter un nombre de ronds différents. Des objets présentant un, deux ou trois ronds sont homologues de ce point de vue. Ici encore il nous sera loisible de différencier des relations d’homologies plus ou moins fines en fonction de ce que nous considérerons comme noué ou non noué. Nous pourrons faire varier l’analyse : — en considérant comme non-noués, c’est à dire neutre quant au nœud, soit les ronds libres entre eux du nœud trivial, soit les ronds enchaînés des non-nœuds de notre théorie des chaînes intrinsèques; — en identifiant les objets selon le choix de l’une de nos différentes théories. Ce moyen conduira à la question de l’hétérologie du nœud, en achevant la formulation de la différence entre propre ou impropre, les enlacements étants présents ou absents. Ainsi, le déploiement et le rassemblement de cette clinique, les conséquences des échanges entre J. Lacan et P. Soury malgré les grandes difficultés rencontrées et l’hétérologie du nœud, feront l’enjeu des deux derniers ouvrages de cette série compte tenu des résultats obtenus aux travers de cette suite à nos différents ouvrages traitant du nœud. 3. Structures freudiennes de la clinique en topologie du nœud Mettons en œuvre maintenant un certain nombre de points de recoupement entre les structures nodales et les structures freudiennes. Il est deux difficultés majeures rencontrées par le débutant lorsqu’il affronte l’approche de la clinique de la psychanalyse par l’espace nodal. L’étude elle-même de ces objets et leur fonction restent problématiques. Mais la première se double de deux aspects. Il y a les résultats en eux-mêmes mais il y a aussi l’usage ou la pratique de cette quête qui présente un lien avec les structures freudiennes de la névrose et de la perversion d’une part, de la psychose d’autre part. Ce sont des styles d’investigations. La seconde difficulté est donc liée à la première. 1 — Au delà du premier aspect auquel certains voudraient réduire nos travaux, nous avons commencé à répondre au second aspect en parlant de lecture. Si pour Lacan, il s’agira qu’au terme soit écrite cette clinique de la psychanalyse telle une orographie indépendamment de l’ancienne nosographie psychiatrique, cette amorce de réponse reste à étayer plus rigoureusement car nous n’en sommes pas encore là et personne n’invente une écriture dans l’isolement. Notre propos reste de pratiquer la lecture et de répondre de la lisibilité de ce qui a été énoncé par Lacan. Car la thèse que représente l’existence de la psychanalyse dans le monde, ce qui n’est pas une hypothèse malgré que ses tenants en soient encore intimidés, c’est qu’il y a du lisible sans même ou avant qu’une écriture soit constituée comme telle. Nous la reprenons maintenant en traitant des traductions, transpositions, transcriptions, en peu de mots : des points de capiton, proposés par Lacan entre le discours de l’analyse et cette topologie du nœud. Et nous répondons déjà à la seconde difficulté. Ce capitonnage se fait selon la structure de la métaphore poétique radicalisée ici en condensation signifiante. Ceci veut dire qu’il n’y a rien à comprendre, il n’y a qu’à suivre Lacan ou ne pas le suivre, et expliquer si nous choisissons de le suivre, au sens de déplier, d’expliciter le paradigme ainsi construit de manière absolue. L’apprentissage est produit par la pratique coordonnée des deux textes sujets à traduction comme dans l’écriture des Japonais. L’étude des nœuds telle que nous y apportons nos soins avec rigueur par le moyen de la ficelle et du dessin. La lecture rétroactive de Lacan et de Freud pour situer ce dont il s’agit et de quelques autres pour se saisir de ce qu’il ne faut pas faire. Car nous en attendons des présentations cliniques renouvelées qui aient une autre visée que de faire croire à la garantie pseudo-médicale de ceux qui s’y exercent jusqu’à aujourd’hui. Ceci dit poliment, nous mettons toujours à part Freud et Lacan. 2 — Pour la seconde difficulté, la fonction qui n’est pas le sens mais qui le produit ici, risque de rester masquée par ce qui reste notre visée majeure, soit la mise à jour de la structure principale du champ freudien dont dépend, du signifiant au symptôme, une quelconque formation de l’Ics et du fantasme à la pulsion la refente subjective. Nous apportons ici quelques éléments supplémentaires à la chaîne des raisons que nous avons tissé, pour notre usage personnel, afin de dire le lien, confirmé par ceux qui le refusent, entre rhétorique et logique. Nous voulons établir cette pratique du dire en formulant la condition rhétorique ou sophistique dans la suite de la condition d’emploi formulée par Tarski du prédicat de vérité. Soit l’établir du côté réel, dans une pratique du narcissisme moins débile de ne plus recourir au seul matériau réduit à des fragments corporels mais à sa corde, autour de ce qui insiste comme impossible, entre intrinsèque et extrinsèque, soit ce qui ne cesse pas de ne pas s’écrire. Nous avons commencé ce tressage dès le premier ouvrage de cette série, avec une définition des plus précises de la fonction du phallus, la dimension du semblant, en partant du fétiche. C’est dire que notre avancée est contingente, due à l’amour et au hasard de la rencontre, puisqu’en cette série un bout de réel cesse de ne pas s’écrire. Les structures freudiennes de la clinique ont leurs transcriptions topologiques dans le discours de l’analyse. Il s’agit d’y situer névrose, perversion, psychose et psychanalyse elle-même dans la pratique. En prenant soin d’en distinguer la folie malgré sa proximité d’avec la névrose sous l’aspect du surmoi et de spécifier la causalité psychique dans sa présentation par la perversion sous l’aspect du fétichisme. Cette introduction à l’Ics et à la sexualité, tels que Freud pouvait les entendre, par la fonction du phallus, la mise en fonction du semblant, nous conduit à préciser la différence entre métaphore impropre et délire propre à la psychose paranoïaque. La structure du fantasme est ainsi encadrée et nous pouvons situer la question de l’objet constructible dans la psychanalyse. 0 - Folie et causalité psychiqueSituer de façon correcte le discours analytique nécessite de distinguer entre folie et causalité psychique. Sans ce rappel à l’entrée du champ freudien, nulle chance de s’y retrouver dans la structure. Nous en présenterons les termes après avoir rappelé cet axiome déterminant l’évidence fondamentale du discours analytique. Évident au point de rester oublié, voire inaperçu des praticiens eux-mêmes, tombant par là sous le principe de la structure causale dont il va être question par la suite. Nous commençons donc ce chapitre par un rappel de structure qui peut paraître éthique — il l’est en effet — puisque notre esthétique est une éthique. Il s’agit de résolution. De résolution du désir, au sens de résoudre le désir comme se résout une équation en trouvant la solution qui la satisfait, au sens d’un désir résolu dont rien ne saurait détourner le sujet. C’est ce à quoi la névrose répugne. Reprenons les diverses définitions de la folie proposées par Lacan [É a 8]. Folie particulière… Le mammifère humain est xénopathe du fait de sa prématuration réelle. Son état réclame qu’il s’incorpore au discours comme dans un poumon d’acier. Il est donc foncièrement parlé par l’Autre, il est ainsi parlêtre. Mais cette nécessité ne l’oblige pas à se croire être parlé par un autre, première définition de la folie, dans la réalité. Ceci diffère du fait d’être parlé par l’Autre, un lieu de fiction véridique, réelle, plus réel que la réalité. Cette croyance peut s’établir seulement du fait d’une démission. Ce renoncement a un premier nom, la méconnaissance, définition principale de la folie. Ce n’est pas ne pas connaître, c’est refuser de reconnaître ce qu’il connaît très bien, même trop bien. Le résultat de cette esquive par le repentir c’est le moi, cette enveloppe de l’abject m » i (a) où se complaire, le moi est une structure folle.Ainsi le sujet peut s’y croire, deuxième définition de la folie, ou se croire, comme l’on dit dans le sud de la France : “Pour qui-y s’prend?” dit-on. Ça lui va bien. Cet énoncé venant pour une question : “Pour qui se prend-il?” En effet : “Pour qui-y s’croit?” Cette non-reconnaissance aboutit au rejet sur l’autre, sur les autres, par le sujet, de sa propre responsabilité. C’est la politique de la belle âme névrotique, troisième définition de la folie qui rejoint la première. Puisque le sujet est xénopathe, intégralement déterminé par l’Autre, c’est ça l’inconscient, le lieu “là où s’était” nous dit Freud, ce dont je dépens radicalement. Il est bien difficile pour moi de dire “je”, de m’y reconnaître comme responsable, d’advenir comme sujet qui dit “je”. Or “je dois advenir” ajoute Freud. Nous prolongeons la difficulté en ajoutant que cette reconnaissance ait lieu après coup, ce qui ne fournit pas de circonstances atténuantes. Éthique difficile, voire impossible à supporter, sans la notion de la vérité comme fiction recouverte de fixion, soit l’Autre rabaissé à l’autre. Il faut disposer d’un aperçu sur la phonction fallique qui recouvre en un tout ce qu’il n’y a pas. S’il n’en est pas ainsi, c’est la folie, la méconnaissance avec ses contrecoups de culpabilité inconsciente, comme si le sujet s’entendait dire par cet Autre : “Ah oui, ce n’est pas toi! Tu dis n’y être pour rien! Tu dis avoir des circonstances atténuantes! Eh bien, tu vas voir si ce n’est pas toi!” Réponse abjecte et totalitaire de l’Autre. Nécessité structurale lentement découverte par Freud, il lui donne le nom de surmoi, enfin formulée par Lacan. Il s’agit d’une formule aussi réelle que celle de la gravitation universelle. … et folie collective Freud propose de décrire le malaise dans la cité à partir du constat qui n’est pas seulement que la civilisation réclame du sujet qu’il se soumette à la loi de la cité et renonce à son désir. Est-ce son désir? Est-ce ses pulsions? Freud ajoute que plus le sujet cède sur son désir, plus il se soumet à la loi en renonçant à la Loi, plus s’impose à lui l’exigence toujours plus grande, c’est la Loi, de la loi ainsi intégrée. Il n’y a que les petits moralistes qui diffusent l’enseignement de Freud comme névrotisant, ça les arrange dans leur propre façon de satisfaire ce à quoi ils sont soumis, cherchant à se défiler. Créon de nom, l’appelle aux gens bien, sacré nom de non, de non de nom. Lacan de le prolonger [2 Sém 3], car il y a pire, ce dont, contrairement à l’adage, nous pouvons être sûr comme du père. La folie court les rues. Il n’y a pas d’ordre social qui ne repose sur la névrose. Que le sujet se fasse du tort assure la stabilité sociale. Se faire du tore, c’est l’aspect du surmoi dans la névrose, le tort névrotique résultant de la méconnaissance. Et Lacan ajoute, faire du tort aux autres, par quelques paroles assassines, la loi nous en laisse toute l’amplitude. Alternative à l’asile La psychanalyse ne commence que lorsque le sujet renonce à la folie, d’avoir suffisamment débattu de la politique de la belle âme [É a 21]. La non-folie définit la position de l’analysant, c’est ce en quoi la psychanalyse soigne et guérit la névrose. Ceux qui disent le contraire ou sont sceptiques sont des fous qui n’ont jamais rencontré ni Freud ni Lacan ni quelques-uns de leurs élèves ayant tenu le coup sans rien y comprendre. Reste maintenant à la faire, cette analyse, et l’achever dans sa régularité, lui trouver son accomplissement légitime. C’est l’étude, jusqu’à son terme rigoureux pour le sujet lui-même, de la causalité mentale, la sienne propre, pour en faire autre chose que circonstances atténuantes. Compte tenu de ce prérequis, avant d’entreprendre une clinique de la psychanalyse d’où la folie est rejetée, nous proposons ici une clinique des entretiens préliminaires soit une clinique de l’asile, le monde où nous vivons, dominé par l’enlacement, fou. Clinique de l’asile Nos repères de structure nous conduisent à réviser des idées reçues et à en élaborer les objets, car il semble préférable de se référer aux contraintes logiques de la structure comme aux textes de Freud et de Lacan qui ne sont pas encore lus à ce propos, plutôt que de se fier à de vagues impressions que l’on veut nous faire croire issues de l’expérience. L’expérience de chacun, dans le plus grand nombre de cas, ne fait que suivre ce que la rumeur colporte. Vingt années de pratique, en position d’assurer une consultation de psychanalyse, nous ont confirmé là-dessus. Cette rumeur de foule confirme la structure en cherchant à la contredire, elle fait apparaître comme effacé le tranchant de l’épreuve et choque l’expérience personnelle de ceux qui en ont une un peu poussée ou un peu exigeante. Quiconque n’a pas l’intuition clinique de Freud. Il est déjà difficile de suivre le raisonnement, les arguments de Lacan. Il a voulu les choses ainsi pour que l’on ne puisse pas simuler sans que cela se voit. Et ça se voit, ou s’entend. Pourtant malgré cela, Lacan retrouve et situe les flèches freudiennes à leur place. Nous repartirons du treillis des huit théories déjà isolées. Elles répartissent les structures cliniques de l’asile où nous situons les mouvements gordiens. Le mouvement gordien propre est noté H et le mouvement gordien impropre noté G. Le lecteur constatera que les non-nœuds, sous l’aspect de l’enlacement, occupent tous les postes de ce treillis, c’est ce trait qui nous fait parler de l’asile à ce propos.
Commençons par les positions que la psychanalyse a toujours jugé pouvoir traiter. Ce sont les styles dans lesquels la capacité de métaphore du sujet n’est pas complètement détruite, une certaine crédulité y persiste à l’égard du semblant. Nous voulons parler de la névrose et de la perversion opposées l’une à l’autre dans la structure, comme le sont répulsion et attraction. Le tore névrotique La structure de la névrose, c’est la structure du tore. Nous proposons de l’écrire ainsi. Comment lire cet algorithme? Lacan présente la névrose en termes de désir et de demande sur le tore [2 a’ 26]. Le sujet réitère les tours de sa demande sans apercevoir qu’il parcourt du même fait un tour du désir. C’est la dualité des tours méridiens et des tours longitudes pour un sujet qui oublie, du fait de sa position intrinsèque, qu’il est sujet au tore, faute de passer à l’extrinsèque à considérer le tore en objet11. Dans la névrose, la pulsion : ($ à D) vient à la place du fantasme comme cela se déduit par le calcul du mathème. Où, en effet, D, la demande, F @ D et D remplace a, l’objet cause du désir, dans la formule du fantasme. ($ à a) Le sujet de ce faire du tore, par cette méconnaissance du désir dans la demande. La soumission comporte la déresponsabilisation du sujet, sa folie. Ainsi chez le névrosé, le terme - j, négation du pénis comme effet en retour de la négativité recouverte par le phallus, est fixé sous le mathème du sujet $ dans son oscillation entre les deux termes du fantasme. $ __ – j éclairant ce fait clinique que le névrosé a horreur de son nom propre.Il s’agit d’un défaut narcissique qui s’appelle refoulement. Cela crée au sujet quelques soucis relatifs à l’assertion qu’il ne distingue plus de l’affirmation et de la négation. De ce fait, il croit ne pas croire au Père Noël alors qu’il y croit, un semblant qui dure. Puis Lacan va retourner l’affaire, pour finir par dire la même chose à l’envers [É a’ 26, p. 42]. Or la structure torique en termes nodaux, c’est l’enlacement. Marquons cette structure d’une icône.
La variété de l’enlacement est homéotope à la surface torique. Cela veut dire qu’indépendamment de leur dimension, ces espaces ont même groupe fondamental. Nous pouvons y parcourir les mêmes classes de trajets. D’où se déduit notre scription. La structure de la névrose, c’est la structure de l’enlacement méconnu. La structure de la névrose, c’est se faire du tort. Le processus du surmoi comme réponse de l’inconscient. Le sujet se fait du tore par omission de la dimension de l’Autre. L’Autre oublié se rappelle au sujet par la culpabilité symbolique, prenez le bateau qui mérite d’être médité, de la dette du même nom. Le forçage de l’Autre donne le même résultat dans les reproches que le sujet lui adresse ou la causalité qu’il met en lui pour se défiler. L’onanisme a les mêmes effets, en dehors d’une ascèse très stricte, c’est un mauvais service rendu à l’organe du fait de l’impasse faite sur l’Autre, le sujet névrosé croyant arriver plus vite à ses fins. Nous remarquerons de ce fait que la névrose a le même caractère que la folie, comme conséquence de la politique de la belle âme. Le moi est une instance folle avons-nous dit, et la névrose est un malaise du moi fort, irresponsable. Folie surmoïque sur laquelle est venu buter le traitement analytique pour Freud avec la réaction thérapeutique négative qui mettait ses analysants au pied du mur de la fonction phallique. Pour surmonter cette non-issue, il faut un discours analytique plus élaboré entre ses tenants. Même peu nombreux, il faut qu’ils aillent jusqu’à assumer les axiomes de ce discours. Nous parlerons de la folie névrotique, la névrose hystorique que l’analysant se doit de laisser à l’entrée de l’analyse. C’est pour cela que la psychanalyse guérit la névrose, encore faut-il s’y engager, encore faut-il qu’il y ait du discours analytique. Nous parlerons de la folie névrotique de l’enlacement. Nous thématiserons cette folie par la formule métaphorique et scripturale suivante qui domine la civilisation rabaissée au rang de l’asile.
Derrière la folie surmoïque, une voix ajoute : “(j’)ouis moi bien”, toujours le recouvrement. C’est ainsi que la structure se manifeste dans l’histoire, dans le ruissellement, nous parlerons donc de la névrose hystorique dont le prototype est la phobie, la névrose d’angoisse, plaque tournante de toutes les névroses. Les deux grandes névroses, hystérique et obsessionnelle, se déduisent de cette structure grâce à l’éclatement de la formule du fantasme, dans un troisième calcul. Respectivement : — du côté de l’objet a, l’intrigue hystérique qui essaie de relever la sexuation de l’objet du désir, répond à la jouissance qui a été interdite; — du côté du sujet $, avec l’impossible mort du sujet chez l’obsessionnel qui essaie d’empêcher l’évanouissement du sujet en réponse à la jouissance qui l’a submergé. Mais en rester là serait oublier que la psychanalyse est un exercice de lecture, elle n’est pas la recherche d’un modèle. Afin d’entrer dans le champ freudien, il y a le pôle opposé à celui de la névrose, celui de la perversion dont le rôle est précisé par Lacan avec le sinthome comme nous l’avons déjà dit plus haut. Clinique de la psychanalyse Nous constatons que l’enlacement, caractéristique des non-nœuds, occupe tous les postes du treillis d’une clinique de l’asile. La question se pose maintenant de l’existence de théories du nœud indépendantes des non-nœuds. Ce serait une clinique sans enlacements, une clinique de la psychanalyse.
Nous voulons montrer par la suite quelles sont les théories nécessaires lorsque les enlacements sont mis à l’écart par l’enveloppe éthique de l’analyse. Deuxième question mise à jour par notre présentation Pour cela, il faut d’abord étudier en présence de l’enlacement qui fait malaise dans la civilisation, les relations qu’entretiennent ces diverses théories. Passage de l’extrinsèque à l’intrinsèque et passage réciproque le long des arêtes du treillis des théories dans l’asile avec lequel nous n’avons donc pas fini. Il faut poursuivre ce qui a été entrepris ici, isoler des non-nœuds parmi les nœuds. Cette étude qui doit nous permettre de nous détacher de l’asile, va jusqu’à situer la fonction des nœuds de la famille du nœud de Lacan et du nœud trèfle parmi les nœuds propres. Ceci se fait au moyen d’une relation, dite d’homologie, qui va être définie pour conclure ce chapitre et cet ouvrage, et par conséquent de la prise en compte de l’hétérologie du nœud. Cette relation nous conduira à comparer les mouvements gordiens propre (homotopie) et impropre entre eux, dans la suite de cette série. Il y a là matière à revenir sur la notion de croisement dans des cas d’espèces particuliers. Où s’éprouve la difficulté principale d’une présentation clinique d’un cas dans la psychanalyse comme d’un commentaire d’une figure, d’un style, en critique littéraire. Ainsi précisons maintenant le second point que nous soulignons au début de cette présentation des structures freudiennes. Nous disons maintenant ce dont il s’agit dans cette clinique et dans cette topologie qui les fait résonner ensemble. Dimension clinique 0 — Nous avons déjà établi la structure du semblant, celle de la fonction imaginaire du phallus. Elle présente une difficulté, dite aliénation, pour le sujet. En effet, si le sujet adopte l’option mâle, alors il n’y a nulle nécessité (impossible) logique qu’il en soit autrement, seul ce qu’il refoule ainsi fait retour dans ses symptômes. Alors que, s’il opte pour la version femme, en ne refoulant pas la castration, il va la subir, car de l’avoir choisie, autorise sa disparition comme probable (possible) logiquement et le retour nécessaire à la position homme. Il est véridique qu’il soit contingent qu’il y ait des femmes dignes de ce nom. Il paraît qu’il y en a eu à Venise… 0.1 — Le symptôme réalise une figure du discours. 0.2 — Ce n’est pas que le sujet prenne conscience des éléments refoulés, ni de leur sens, qui supprime le refoulement. Il peut y avoir une levée (Aufhebung) intellectuelle du refoulement grâce à la négation classique mais pas une acceptation (Annahme) affective du refoulé. Ainsi nous sommes amenés à insister toujours sur le trait caractéristique de notre analyse de la dénégation, sur ce qui reste inaperçu, chez les élèves de Freud et de Lacan. Il y a une ambiguïté, à propos de la fonction de marqueur qu’a le signe de la négation, dans la lecture que nous pouvons faire du texte de Freud. Or, inversement, il s’agit toujours pour le sujet de faire tenir ensemble, dans une même construction syntaxique, les deux termes d’une contradiction plus (forclusion) ou moins (refoulement) exclusive. Dans le cas contraire… “Un contenu de représentation ou de pensé refoulé peut donc se frayer passage (durchdringen) jusqu’à la conscience, à condition qu’il se laisse nier. La négation est une manière de prendre connaissance du refoulé, à proprement parler, elle est déjà une levée (Aufhebung) du refoulement, mais certainement pas une acceptation (Annahme) du refoulé.” Il y a la fonction de la négation qui apparaît comme marqueur donc et cette différence entre levée et acceptation du refoulé. Nous parlerons de l’emploi de différentes négations mais cela doit se démontrer en bonne logique. L’enjeu est précisé par Freud. “On voit comment ici la fonction intellectuelle se dissocie du processus affectif. Avec l’aide de la négation, on ne fait faire marche arrière qu’à l’une des suites du processus du refoulement à savoir que son contenu de représentation ne s’étend pas jusqu’à la conscience. Il en résulte une sorte d’acceptation (Annahme) intellectuelle du refoulé cependant que l’essentiel reste soumis au refoulement.” Cette différence, entre levée et acceptation, devient ici la distinction entre fonction intellectuelle et processus affectif. 0.2.1 — Nous revenons sur ces distinctions entre levée du refoulement et acceptation du refoulé, fonction intellectuelle et processus affectif, parce que c’est précisément l’aspect rhétorique du symptôme, son aspect stylistique et non-classique, au sens logique, qui fait conclure à la dissociation du processus affectif et de la fonction intellectuelle. Loin que les mots expriment les idées, les phrases manifestent les pensées, et les figures révèlent les sentiments ou les passions voire les affections, c’est plutôt ces catégories de langue qui produisent leurs effets jusque dans le narcissisme et font croire à l’existence parallèle de ces entités de l’esprit. Or nous avons déjà assez à faire avec le décryptage des fictions véridiques produites par l’emploi rhétorique effectif de la langue pour ne pas avoir à fabriquer des fantômes supplémentaires. C’est, au contraire, l’incidence du dire dans son effectivité qui fait supposer ces suppléments psychologiques suspendus aux murs d’un lieu improbable comme des portraits de famille dans une sombre demeure. Il faut bien que l’illusion du moi (onto) trouve son logie, refusant de se reconnaître dans les mots (risque de délire interprétation), les phrases et surtout les figures, il se place de l’autre côté, dans ce qu’il croit être, ses idées, ses pensées et ses passions. 1 — Ainsi plus que de l’intérêt que le sujet pourrait porter à son propre style, le transfert révèle chez lui une passion pour le principe (Œdipe) auquel doit satisfaire une figure afin de passer pour rhétorique. Passion attractive et répulsive qui fait croire le sujet à la dimension naturelle voir surnaturelle de son attachement à ses figures privilégiées et méconnues. Méconnues, c’est-à-dire plus ou moins confusément connues et reconnues Il nous faut donc revenir sur ce qu’est un style, une figure, un procédé littéraire. L’enjeu clinique se trouve dans l’importance de la structure logique de ces figures insoupçonnées par le sujet lui-même. Mais la question rebondit de la différence du sens au style à la différence entre rhétorique et logique Certains tiennent ces deux disciplines et les contraintes qu’elles étudient pour radicalement différentes, voire incompatibles. Il nous faut dire pourquoi ce n’est pas le cas, puisqu’elles compatissent, mais oui elles compatissent. 1.1 — Ce principe relève d’une involution, propre à la vérité. Principe La difficulté à savoir, présentée par la vérité, la rhétorique et le dire, tient, pour le commentaire érudit de la subjectivité scientifique, à l’absence de marqueurs qui attestent la présence de la vérité, de figures ou qu’on dise tout simplement. Nous pouvons toujours tenter d’introduire de manière savante de tels marqueurs qui indiquent par exemple la présence d’une métaphore dans le vers de V. Hugo proposé par Lacan : « Sa gerbe n’était ni avare ni haineuse. » Si nous marquons (linguistique) cette figure à l’aide d’un prédicat de métaphore comme : « Sa gerbe » est une métaphore ce prédicat doit être susceptible de répondre à la condition (rhétorique) de structure T : « sa gerbe » est une métaphore de sa gerbe. le connecteur de l’équivalence logique « Û » se lit « si et seulement si ». Car ce qui fait la force d’une figure, c’est de nous surprendre d’une façon spéciale, qui tient précisément à l’absence de marqueur. Ainsi, du fait de cette condition, les figures du discours sont comme les occasions de situer la subjectivité dans le langage [41] lors de l’emploi des pronoms personnels, de la deixis et des performatifs. Ce principe propre à la vérité (Tarski), quoique crucial en logique, n’est déjà pas très étudié dans cette discipline où les logiciens préfèrent interroger l’aspect syntaxique des énoncés apparemment plus proche de l’algèbre. Que dire des linguistes qui ont su introduire grâce à ce privilège de l’ordre un peu de raison dans leur domaine mais qui, aujourd’hui, n’osent plus prolonger cette avancée dans la bonne direction. Tributaires des professeurs de philosophie, les uns et les autres sont contraints de participer au sauvetage désespéré de la conscience. Pacte criminel dont nos savants sont les otages. Il se traduit par une absence de critique de la psychanalyse pertinente quant à sa raison. Ce principe lié au dire qui fait impérative chaque énonciation, joue à l’occasion de chaque figure pour la produire comme figure, avec la présence liée à la plasticité du signifiant et l’absence de marqueur à laquelle supplée le fait de dire qui l’impose d’abord. D’abord veut dire, avant une quelconque critique, discours du maître qui légifère toujours même là où il est périmé. 1.2 — Nous avons déjà étudié la vérité et le marqueur de la vérité. La négation apparaît classiquement comme le marqueur de ce qui est faux. 1.2.1 — Nous retrouvons ainsi la fonction de la négation qui est une fonction de marqueur, déjà relevée par Freud. Ce qui est faux serait la même chose que ce qui est refoulé. L’Ics de Freud est cette antinomie. Or ce qui est refoulé est non-vrai et irréfutable. 2 — La figure comme la vérité est le recel d’une inversion sur fond de dissolution. Cette rupture de semblant provoque un ruissellement de lettres qui ravinent le signifié. À le décompter se produit le ravissement, retour au semblant qui lie. 2.1 — La construction de cette involution nécessite le plongement d’un objet dans un espace de dimension plus élevée. 2.2 — La dimension est un invariant topologique. 3 — L’ensemble de ces énoncés forme une chaîne de raisons qui situe l’aspect incontournable pour l’analysant de cette structure topologique investie à l’ordinaire dans le narcissisme. Nous appellerons cette structure de l’involution signifiante, copule qui unit l’identique avec le différent, la structure du semblant, notée F, dans le discours de l’analyse, et qui domine le fonctionnement du –j dans l’image du corps. 3.1 — D’où se découvrent deux modes de satisfaire à une fonction, deux jouissances liées au corps. C’est la raison de cette distinction, du côté de la structure plus que du ruissellement que reprend Lacan entre les chaînes borroméennes à trois et celles à quatre ronds. La perversion, le sinthome Nous voici ramenés au lien établi par Lacan entre la perversion et l’involution du nœud entre la chaîne à quatre ronds et la chaîne à trois. Nous ferons des chaînes à quatre, l’objet de l’ouvrage suivant12 dans la série. Pour ce qui nous intéresse dans cet ouvrage, nous retiendrons l’effet de cette involution parmi les objets construits avec un, deux ou trois ronds. Car cette structure a une réalisation dans le trois. C’est la question du borroméen généralisé. Nous la développerons dans le dernier ouvrage13 de la série. La structure de la perversion, c’est le sinthome quaternaire. Ainsi nous proposons d’écrire cette figure de la père-version (réalité) par un nœud :
compte tenu de l’effectivité de la chaîne à trois qui reste cette fonction impensable du père. Comment lire cet algorithme car la structure de la perversion c’est le fétichisme. Articuler de façon rigoureuse le sinthome comme tendance vers le père au fétiche, nécessite d’avoir établi la fonction du semblant, comme nous l’avons fait avec Hans et Tarski. La lecture que nous proposons de la perversion dans les Écrits de
Lacan se confirme si nous nous reportons à son mathème tel qu’il le propose [É a
29, p. 823]. Il s’agit bien du fétiche lorsque a remplace D’autre part, il y a une constance chez Lacan, constance qui se confirme par la fixation du vocabulaire dans les dernières années. Le quatrième terme prend bien le nom du troisième mode de l’identification primaire, dans l’équation souvent reprise : symptôme = amour pour le père Une question principale se pose à la lecture des Écrits de Lacan si on y regarde de près, à propos de cette association de la fonction paternelle à la perversion, mais sa réponse devient lisible. Si la structure de la perversion, c’est le fétichisme, le fétichisme, c’est l’instauration du semblant au sens de la métaphore. Structure maîtresse du langage parce qu’ayant trait à la vérité. Lacan en fait même le discours du maître, entre le tout du vrai qui s’impose de manière impérative dans l’assertion et le pas tout d’une parole véridique. Nous avons montré par Hans et Tarski pourquoi il faudrait qu’il y ait un pénis là où il n’y a rien. Les structures freudiennes de la clinique, tendues entre névrose et perversion sont mises en œuvre par Lacan dès son séminaire traitant de la relation d’objet [2 Sém IV]. Il s’agit bien de l’opposition, absolue dans la structure, de la phobie et du fétichisme. Elle se module bien sur l’opposition de la métaphore et de la métonymie. La première question se trouve entre métaphore et métonymie. En effet, nous associons ici le fétiche à la condensation signifiante alors que Lacan » [É a 32, p. 877], lorsqu’il décrit les conséquences de la découverte de l’absence de pénis chez la mère, emploie l’expression opposée au fait de « se remparder d’une phobie » qui est celle de « restituer le fétiche quoique déplacé ». Condensation ou déplacement, névrose ou perversion, ces oppositions sont susceptibles comme chaque couple d’opposition chez Lacan, d’une involution. Nous répondons toujours par l’involution signifiante au lieu de certitude, mais cette réponse est légitime après que nous en avons dressé la doctrine en logique mathématique. Alors, mais alors seulement, nous pouvons assumer le fait que Lacan effectue au cours de ses Écrits et de ses séminaires une involution entre métaphore et métonymie, dont la ligne sans point se situe dans un Écrit. Il s’agit de « Radiophonie », lorsqu’il répond à la troisième question qui lui est posée à propos de la linguistique. Nous ouvrons ainsi la voie à un commentaire de cette réponse selon la raison qui a conduit à la formuler telle qu’on peut la lire. Dans la structure, il y va de la pulsation entre borroméens :
Dans ce qui précède, il y a de la métaphore, elle joue un rôle d’effectivité au regard de quoi les autres structures se déterminent. La métaphore impropre La métaphore du nom du père satisfait une fonction particulière dans le discours de la psychanalyse. Notons ce résultat de la manière suivante :
Cette fonction est celle de l’effectivité de la chaîne à trois. Nous voulons dire la fonction effective du trois borroméen en tant qu’il suffit, avec le mouvement nœud quelconque, à détruire ou construire n’importe quel objet qui n’est pas un non-nœud. En tant qu’il s’agit de plonger la théorie des non-nœuds dans la théorie du nœud. Or à partir de là l’analyse consiste à diffracter ce plongement en divers théories, caractérisant des n espaces, grâce à la spécification des différents mouvements nœuds. Dans la chaîne borroméenne à quatre ronds, le nœud qui tient les trois ronds dans la chaîne à trois est explicite. Le sinthome écrit ce qui est implicite dans le trois, elle passe alors pour ce vers quoi tend sans y parvenir le quatre, le sinthome, la perversion. Ainsi nous écrirons aussi bien :
Lacan explique sa tentative en relevant que Freud s’en tient au quatre dans Totem et tabou principalement, et il a besoin du mythe du père Orang-outang là où la structure montre une autre raison au meurtre avec le passage du quatre au trois. Le mathème de la métaphore subit des variations dans les Écrits de Lacan, dont nous retenons la dernière formule :
S’il se trouve que c’est le discours du maître, c’est bien du fait impératif du signifiant articulé par cette formule. Encore la fonction du dire. Nous l’écrirons donc de ce nœud, ayant établi sa fonction dans la topologie.
Nous calculerons maintenant dans cette topologie du nœud le rapport à la métaphore qu’entretiennent le fantasme et le délire. Ce calcul tient aux sections transverses. La rigueur de ce calcul repose sur la relation d’homologie dont nous voulons mettre la définition en train pour conclure. La structure du fantasme Mais d’abord la structure du fantasme. Elle s’écrit :
La chaînœud de Whitehead est obtenue de la chaîne borroméenne par une section transverse. Nous pouvons lire la fonction des chaînes de cette famille dans le treillis des théories. L’écriture mathématique du fantasme par la formule : ($ à a) fait supporter par le connecteur ¹ la relation qu’entretiennent ses deux termes, le sujet et l’objet. Cette relation se trouve dans la réversibilité des deux ronds de la chaîne en question [2 Sém XX, Encore].
Le rond plié peut être déplié à condition que l’autre rond soit plié à son tour à la manière du précédent. C’est la réversibilité des ronds, une telle chaîne sera dite réversible. Ce n’est pas le cas de toutes les chaînes que nous définissons comme étant de la famille de la chaîne de Whitehead, si nous les caractérisons comme étant des 2-chaînes issues de 3-tresses présentant une partie paire et une partie impaire (nous voulons parler des parties coupure ou non-coupure de notre description graphique achevée au chapitre VI). Nous étudierons leurs rapports aux chaînœuds borroméennes grâce à l’homologie définie plus loin. Elles sont des chaînœuds généralisées, mais passablement altérées, il reste toutefois une trace de l’opposition des parties, opposition nécessaire aux chaînœuds. Passons maintenant au défaut de métaphore avec la poursuite de l’altération jusqu’à l’effacement intégral d’une des parties de la chaînœud au profit de l’autre produisant ainsi des pur-nœuds propres ou des non-nœuds propres. a2 - Causalité psychique avec altération de la métaphore Il y a deux aspects à distinguer dans l’étude des psychoses. Ces deux aspects sont supplémentaires, dans des dimensions autres dans le treillis des théories, à la pulsation de la structure qui caractérise l’analyse dans les termes avec lesquels nous formulons cette clinique maintenant. Il s’agit du délire et de l’absence de métaphore. Le délire de la psychose paranoïaque Le nœud propre du délire paranoïaque nous porte à écrire :
Nous en avions traité en termes de trou dans la période des surfaces avec le schéma I construit par Lacan pour illustrer son analyse du cas Schreber. L’homologie nous permettra de préciser cette fonction des nœuds propres, présentée ici grâce au nœud trèfle. Dans la psychose, il n’y a pas de signifiant d’un manque dans
l’Autre S ( S (A) º F º a par défaut de la circulation de –j. Nous précisons donc maintenant en présentant la psychose paranoïaque comme congélation du signifiant avec la mise en continuité des trois consistances de la chaînœud borroméenne, le réel, le symbolique et l’imaginaire. Le terme –j traduit donc la distinction des trois ronds dans leur homogénéité [2 Sém XXII, R.S.I.]. C’est cette homogénéité qui n’est pas identité ni mise en continuité dans la chaînœud qui fait difficulté aux élèves de Lacan de la génération qui nous a précédée, comme plusieurs m’en ont donné un témoignage personnel. Le nœud de trèfle est produit par la mise en continuité des ronds de la chaînœud grâce à deux sections transverses. C’est un nœud propre homologue à la chaînœud comme nous le verrons par la suite :
La subjectivité scientifique est propice à rendre courante cette issue, ce style un peu figé, voire carrément bloqué. La subjectivité scientifique Nous retrouvons ce dont nous étions partis au début de ce chapitre avec la subjectivité délirante. Elle se caractérise de trois traits, un délire, un alibi et une croyance, qui la situe dans l’ordre de la psychose sociale. Cette absence de métaphore propre au délire est donc plus étendue au-delà de la psychose paranoïaque. Mais il faut préciser que les mathématiques, si elles sont un discours sans métaphore, ne sont pas pour autant le lieu d’une absence de condensation au sens freudien, c’est-à-dire une rigidité de style. Au contraire, les mathématiques de mathématiciens, pas celles des apparatchiks ou des technocrates, font pure condensation, réduite à la lettre, ce que la langue déploie en métaphore. C’est dire qu’il y a un lien entre syntaxe et rhétorique. Mais la psychose sociale répandue à partir de la pratique scientifique nécessite sa résolution dans l’analyse par la réponse rigoureuse aux questions maintenant posées dans ces termes. Il y a donc lieu de répondre par le mathème. Dans l’écriture mathématique du non-rapport converge le seul lieu où la psychanalyse confine à concurrencer la science. a3 - Causalité psychique et condensation Ces précisions étant apportées, nous pouvons revenir sur un point crucial à l’époque de l’achèvement de la psychanalyse. Après Lacan, une tâche reste à accomplir. Une autre question se pose en effet, qui a été laissée en suspens, à propos de la perversion. Lorsque le lecteur se demande ce qu’il en est du fétiche dans le sadisme qui passe usuellement pour une perversion. Freud le considère comme tel. Dans le sadisme c’est le pervers lui-même qui se fait fétiche. Précision apportée par Lacan, il l’explique dans son Écrit intitulé Kant avec Sade. Mais il nous faut considérer plus que l’instrument privilégié de la perversion. Celui-ci a une fonction. Il s’agit de le faire satisfaire à la structure du fantasme. Ainsi le pervers sadique tente avec cet objet d’atteindre le sujet des tourments qu’il inflige. Ce sujet c’est l’autre pour lui qui est réduit à la fonction d’agent. Il essaie de l’atteindre dans sa subjectivité, c’est à dire sa refente. Si le sujet s’évanouit, la scène se rompt. Mais ici se présente le risque d’une grande confusion que n’ont pas su éviter les élèves de Lacan qui nous ont précédés. L’objet de la psychanalyse Nous écrirons l’objet a, d’une dernière formule algorithmique :
Cet objet est l’argument d’une fonction de détachement caractéristique de la position du sujet désirant. Ainsi il ne faut pas confondre, comme la plupart des prétendants à la fonction de psychanalyste le font, entre le pervers et le désirant. Le désirant ne recule pas devant l’aperçu du manque dans l’Autre, même dans les occasions où il est rabaissé à ce qui s’en perçoit, ce que Lacan formule d’une écriture : a __ -j où le -j du ruissellement de la castration… vient se glisser sous l’objet a. Le sujet désirant dont Lacan désigne l’exemple dans le personnage d’Alcibiade à la fin du Banquet de Platon, illustre par là le ressort et l’issue du transfert. Le désirant est bien dans une position radicalement opposée au pervers puisqu’il se soumet lui-même à l’épreuve de la structure au lieu de tenter d’y soumettre autrui en lui faisant éprouver ce manque. Il vise à jouir du fait d’assister à cette épreuve dans l’autre, au lieu de se soumettre à l’épreuve du ratage du manque dans l’Autre. Notre sinthome pervers est ici très proche de la folie. Cette écriture montre aussi l’opposition avec le névrosé pour qui ce terme –j est inscrit comme nous l’avons déjà précisé sous le mathème du sujet : $ __ - j Mais du même coup cette écriture favorise le risque de confusion que nous dénonçons ici chez les lecteurs de Lacan entre pervers et désirant. Puisque névrose et perversion s’opposent comme des contraires avons-nous dit, comme métaphore et métonymie aussi dans une structure tournante. Cette opposition névrose/désir peut prêter à confusion et ça n’a pas manqué. Voir les rappels à l’ordre de certains petits lacaniens pour que leurs collègues, toujours les autres, ne glissent pas à la perversion en se faisant les héros du désir. En fait il s’agit toujours, au-delà du contrôle de mise au pas, par des pervers eux-mêmes. Erreur commune donc, que de confondre pervers et désirant, dont bien peu se sont privés en ce qui les concerne eux-mêmes dans la tentative de mise en coupe réglée du champ freudien, après Lacan. Ce sont les risques de l’imitation dans ce domaine, il est des actes qui ne se miment pas. Nous revenons à l’analyse pour conclure, à sa fin. Elle est caractérisée par la reconnaissance d’un manque radical que le sujet peut affronter : S ( où ($ à a) où a n’est pas remplacé par D comme dans la formule de la pulsion, produisant une substitution caractéristique de la névrose. Cette restitution des lettres à leur place vaut pour la reconnaissance de l’objet. Enfin construit comme agent, nous écrivons cet objet a, après involution, grâce à un non-nœud qui ne doit rien à l’enlacement. Il s’agit du nœud de Lacan [2 Sém XXII].
Mais ne croyons pas en avoir déjà fini avec le tore de la folie névrotique, c’est-à-dire avec l’enlacement. Il agit encore dans ce contexte de manière sourde et fait courir au sujet le risque d’y revenir à chaque instant. Notre tâche consistera maintenant à le repérer au bon endroit. À cette fin nous voulons comme première étude, revenir à la différence des approches de Lacan et de Soury. Soit à la comparaison des mouvements gordiens propre (homotopie) et impropre.
P. Soury, en traitant des chaînes à homotopie près T ph, se plaçait dans la perspective strictement freudienne. Il faut voir qu’il est nécessaire d’entreprendre dans le même temps l’étude de la théorie Tp car une involution se joue entre ces deux théories du fait du mouvement borroméen généralisé, soit le mouvement nœud hybride.D’après nos lieux de capitonnage entre théories du nœud et discours analytique, nous constatons alors qu’il s’agit du lieu privilégié de l’étude des névroses et des perversions d’où Freud est parti pour inventer la psychanalyse. Lacan a pratiqué la théorie T ih, à gordien impropre près, dans la solitude du fait qu’il n’a pas suffi qu’il le dise pour que quiconque, à l’époque, s’en rende compte. Pour les même raisons il nous faut nous tourner, de ce côté, vers la théorie Ti, qui est en involution avec celle-là par mouvement hybride interposé.Il s’agit du lieu structural de prédilection du délire et de la folie entre paranoïa et subjectivité délirante dirons-nous. Ainsi se trouve, que participant d’un discours, Lacan du discours analytique, Soury de la subjectivité scientifique, chacun traite plus particulièrement du discours supplémentaire à celui dont il relève, celui dont relève l’autre. Troisième question mise à jour par notre présentation Si nous suivons le treillis des théories auquel nous sommes arrivés, nous pouvons faire apparaître le chiasme qui faisait difficulté à l’époque et qui doit être pris en compte entre gordien propre (homotopie) et gordien impropre. Ce chiasme a une raison sous les traits du mouvement borroméen généralisé, le mouvement hybride encore une fois. Nous pouvons établir ainsi, quelques quinze années après, quelle fut notre intervention dans ce débat. Il sera bien évident à quiconque, que nous ne comprenions pas à cette époque ce qui se tramait là, mais qu’avec de robustes catégories comme celles produites par Lacan, nous pouvons errer dans ce champ de manière pertinente. Sans les risques de fausse prudence que font courir aux autres les prétendus gens sérieux de la réal politique. L’analyse structurale demande du temps afin d’être éclairée, comme l’analyse politique ou l’analyse historique. Ce chiasme concentre ce que le nœud a d’hétérogène par rapport à l’homologie que nous voulons établir maintenant entre les théories. Nous reprenons le chemin de l’Esthétique de cette lettre, après être passé par ce cap difficile où il fallait inverser quelque chose dans l’étude de ces théories. Nous obtenons donc le diagramme suivant pour l’étude de l’homologie.
Nous voici à pied d’œuvre pour étudier l’homologie annoncée dans son lieu, entre ces deux théories T i et Tp.a1 - Homologie (rappel en général) Afin de définir une dernière relation d’équivalence entre les objets de nos théories du nœud, relation qui va produire une équivalence indifférente aux nombres de consistances de ronds enchaînés ou noués, rappelons une notion déjà présentée 14 dans notre ouvrage précédent. Il s’agit de l’homologie des trajets dans les surfaces topologiques.Considérons deux trajets orientés à la surface du tore simple :
Hors la raison intuitive, que nous pouvons avoir du fait que ces deux trajets, dans notre exemple choisi à cet effet, se ressemblent de quelque manière, eu égard à la surface du tore dans laquelle ils sont plongés, nous voulons définir cette ressemblance. Cela revient à préciser de quelle manière ils se ressemblent au point de pouvoir être identifiés dans une classe d’équivalence. Ceci nécessite que la relation qu’ils entretiennent soit une relation d’équivalence. Nous verrons cela plus loin. Appelons a et b nos deux trajets orientés donnés en exemple et considérons maintenant le cas des deux trajets a et – b :
où le signe moins indique un changement d’orientation du trajet, rendu par une flèche sur le dessin. C’est à composer ces deux objets a et – b :
selon un mode de composition qui rappelle nos sections transverses, que nous définirons la relation qu’ils entretiennent. Nous les sectionnons tous deux pour les réunir par une bande dont le bord fait un aller-retour. C’est une portion de surface orientable donc, de manière à réaliser un nouveau trajet nommé (a – b). Cette composition est effectuée, dans les cas où les orientations respectives des deux trajets le permettent, et compte-tenu de la surface où nous construisons ce composé. Si alors, ces conditions étant déjà respectées, le trajet composé est le bord d’un disque, d’une portion de sphère qui peut être prélevée de la surface où nous sommes placés, ce qui est le cas ici :
Nous dirons que (a – b) = d et que les deux trajets a et b sont homologues. Définition Deux trajets orientés sont homologues dans une surface topologique si le composé de l’un avec l’inverse de l’autre forme un bord (de disque). Remarquons qu’à considérer les bords de disque comme une classe jouant le rôle d’élément neutre pour la composition, la relation construite géométriquement entre trajets orientés s’écrit entre classes de trajets (a*– b*) = 0 et produit une structure de groupe entre ces classes. Alors la relation d’homologie entre deux représentants de deux classes d’homologie s’écrit : (a – b) = 0, soit (a – b) + b = b, soit a = b où le lecteur peut se saisir de la nécessité d’introduire l’inverse d’un des trajets dans la définition. Donnons encore un exemple d’homologie à la surface du tore présenté comme sphère à anse. Il s’agit de montrer que le composé de deux trajets est bien homologue à un trajet unique. Soit deux trajets orientés et leur composition selon le procédé que nous venons de décrire :
Ce composé est équivalent par des déformations intuitives au trajet suivant :
Pour nous assurer que cette équivalence intuitive est bien contenue dans la notion d’homologie, considérons le composé de nos deux trajets de départ avec l’inverse de son supposé semblable :
En effet le composé des trois est bien le bord d’un disque : 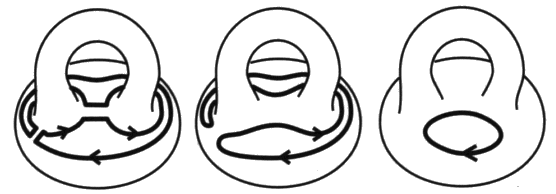 Fig. 43 Fig. 43
Reprenons cette notion intuitive dans nos considérations nodale, afin de préciser la définition d’une nouvelle relation d’équivalence qui comme l’homologie des trajets va faire fi du nombre de composants de chaîne et nous permettre de comparer nœuds propres et chaînœuds. a2 - Trivialisation par symétrie Il arrive, mais cette qualité n’est pas nécessaire, qu’une chaîne S r de r ronds soit telle que, lors de la composition avec la chaîne qui lui est symétrique Sr–1 = sym (Sr) (dans une symétrie d’axe) :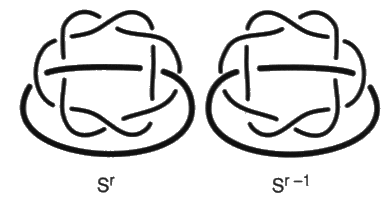 Fig. 44 Fig. 44
grâce à r rubans qui respectent les coloriages des surfaces d’empan des deux présentations données, nous notons # r la composition :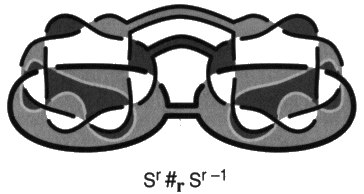 Fig. 45 Fig. 45
L’ensemble se trivialise en r ronds disjoints, non enchaînés, que nous notons e r. Nous attirons votre attention sur le fait que nous avons indiqué la coupure dans cette configuration pour rappeler que le montage se fait de manière cohérente quant au coloriage, mais il ne s’agit pas d’un rond supplémentaire de bord qui insiste. Il s’agit d’un bord qui consiste15.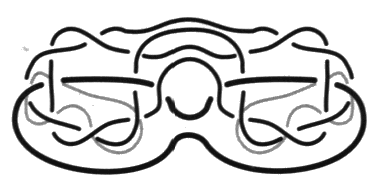
C’est dire que nous pouvons écrire à propos de cette construction : [(S r) #r (Sr–1) = er]Le nombre de rubans et le nombre de ronds Lorsque cette trivialisation ne se produit pas, nous pouvons ajouter r’ rubans tel que nous obtenions : [( Sr) #r+r’ (Sr–1) = er+r’]Ceci nous donne une première indication relative au montage régulier d’où provient un objet considéré. Les rubans supplémentaires seront une indication pour chercher une r+r’-chaîne qui entretient avec la chaîne donnée le type de relation d’homologie que nous voulons étudier ici. Mais cette indication est insuffisante, car il se peut qu’une solution supérieure en nombre existe, même lorsque r’ = 0. Il peut y avoir d’autres solutions avec r’ > 0, avec des changements de présentation des chaînes mises en cause. Définir, selon un procédé analogue à l’homologie des trajets dans une surface, à partir de cette trivialisation, une première relation entre les nœuds et les chaînes, et entre les chaînes elles-mêmes, nécessite quelques précisions. Définition d’un système de sections transverses Nous notons c q un système de q sections transverses qui respectent un coloriage de la surface d’empan d’une présentation de chaîne ou de nœud. Ces sections sont effectuées entre les ronds qui constituent des bords qui insistent de la surface d’empan.
Fig. 47 Nous proposons que ces sections suivent des frontières de la surface d’empan, non des bords qui consistent, c’est-à-dire sans torsion, même non apparente 16.Définition d’un système régulier de sections transverses Un système c q de q sections transverses est régulier pour une r-chaîne donnée avec 0 £ q < r, lorsque pour un ordre quelconque sur cq il fait passer de la r-chaîne à une (r – 1)-chaîne, à une (r – 2)-chaîne… jusqu’à une (r – q)-chaîne.Pour répondre à cette exigence, chaque section transverse est effectuée entre des couples distincts de ronds de la chaîne. a4 - Les sections qui n’entravent pas la trivialisation Définissons alors une relation entre chaînes et nœuds qui utilise les montage par des rubans, la trivialisation et ces systèmes de sections. Définition de la relation d’ordre de degrés m : notée £mNous dirons que deux nœuds ou chaînes S n et Sm, avec n £ m, définis à des mouvements de Reidemeister près, sont liés par une relation de type £m, ou encore que (Sn £m Sm), si et seulement si : Sn = Sm + c(m–n) et, si [(Sm) #m (Sm–1) = em], alors [(Sn) #m (Sm–1) = en].Le système de section c (m–n) n’entrave pas la trivialisation définie par le montage [(Sm) #m (Sm–1) = em]. a5 - Nombre de ronds de la chaîne maximaleMême dans les cas où il suffit de prendre le nombre de rubans égal au nombre de ronds pour qu’une chaîne se trivialise avec son opposée, ce que nous écrivons ainsi avec la relation £r : (Sr) £r (Sr) Û [(Sr) #r (Sr–1) = er]Nous pouvons nous interroger sur le nombre de ronds maximum, s’il existe, et le nombre de rubans nécessaires que nous retiendrons dans la théorie après discussion du cas, soit tel que : (Sr) £max (Smax)Nous obtenons ainsi une seconde indication relative au montage régulier dont provient un objet considéré. Pour un nœud ou une chaîne de r ronds, le nombre p de parties (nouage et non-nouage) peut nous servir de seconde indication compte tenu de la description des chaînes et des nœuds que nous avons déjà proposée au chapitre VI de cet ouvrage. Dans ces conditions, si S max est une chaîne Sm dont le nombre de ronds est m alors ce nombre est tel que : p + 1 £ ma6 - Chaînes partielles d’une chaîne donnée Afin de formuler la présence hétérogène du nœud dans les non-nœuds à partir de trois ronds, nous pouvons considérer, dans une chaîne, ses chaînages partiels ou chaînes partielles. Une chaîne partielle est caractérisée par un quotient de l’ensemble des coloriages d’une chaîne donnée. Lorsque nous considérons la partition la plus discrète de cet ensemble de coloriage, chaque coloriage correspond à ce que nous appellerons des nœuds partiels de la chaîne donnée. C’est dire que dans le cas du nouage de la chaîne dans son ensemble pour chaque orientation fixée, c’est-à-dire la chaîne elle-même, mais dont les orientations des ronds sont rendues solidaires par cette fixation même, nous parlerons des nœuds partiels de la chaîne donnée. Ce sont ces objets partiels qui rendent raison de la présence de nœud dans les non-nœuds. Les non-nœuds présentent aussi des nœuds partiels homologues aux nœuds triviaux. Il est bien évident que le choix de la présentation et de l’orientation de l’objet intervient dans le fait d’établir cette relation d’homologie. a7 - Définition de la relation d’homologie et nœuds homologues Définissons le type de relation d’homologie que nous utilisons ici afin d’isoler le nœud. Définition de la relation HSn Nous dirons que deux nœuds ou chaînes S et S’ définis à des mouvements de la théorie T près, sont homologues dans T ou liés dans T par une relation de type HSn ou encore que (S HSn S’), si et seulement s’il existe une n-chaîne Sn telle que : S £n Sn et S’ £n Sn c’est dire qu’il existe cp et cq : S = Sn + cp et S’ = Sn + cq et si [(Sn) £n (sym (Sn))–1 = en] alors : [(S) £m (sym (Sn))–1 = e(n–p)] et [(S’) £n (sym (Sn))–1 = e(n–p)] a8 - Propriétés que nous voulons étudier par la suite Invariance du nombre de nœud Il est très clair et simple de se saisir du fait que si ces coupures préservent le nombre de nœud nous sommes comblés d’aise. Mouvements homologues Il arrive aussi qu’entre les théories Ti et Tp, les homotopies qui trivialisent un objet de la théorie Ti en son non-nœud contenu soient homologues aux gordiens qui trivialisent une chaîne de la théorie Tp, homologue à cet objet, également en son non-nœud contenu. Nous pouvons considérer alors que d’une certaine manière, à préciser dans la suite, les homotopies sont des moitiés de gordiens. Nous pouvons achever cet ouvrage sur ces perspectives avec une première esquisse de résultats qui font apparaître le rôle des nœuds de la famille du nœud de Lacan dans cette théorie de l’homologie en contraste avec le nœud borroméen généralisé qui, lui, joue un rôle plus proche de l’hétérologie. a9 - Série de chaînes et de nœuds homologues Pour finir nous donnons la série principale de pur-nœuds trèfles et Lacan (nœuds propres) qui sont homologues aux Whitehead dans la théorie T i (2-chaînœuds) et les borroméens (3-chaînœuds), homologues aux mêmes Whitehead dans la théorie Tp.Les objets homologues se correspondent terme à terme en fonction de leur place, d’une planche de dessins à l’autre.
© 1999 Topologie En Extension . Tous droits de reproduction et de représentation réservés. Tous les textes, dessins et graphiques reproduits dans cet ouvrage sont protégés par des droits de propriété intellectuelle détenus par Topologie En Extension. Par conséquent, aucun de ces éléments ne peut être reproduit, modifié, transmis, rediffusé, traduit, vendu, exploité commercialement ou réutilisé de quelque manière que ce soit sans l'accord préalable écrit de Topologie En Extension. |
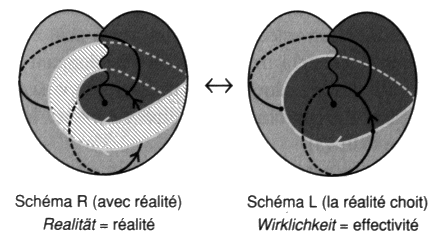 Fig. 1
Fig. 1 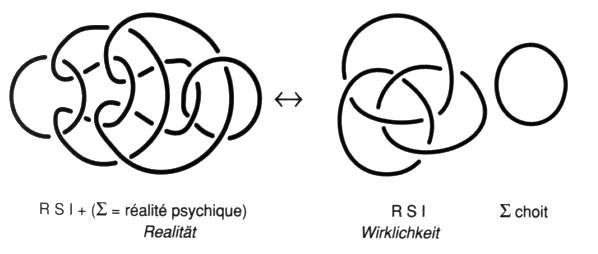 Fig. 2
Fig. 2 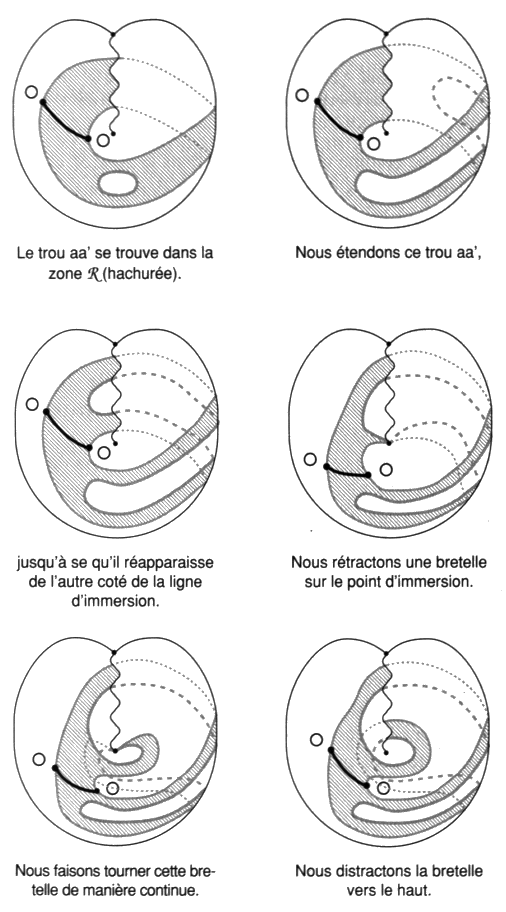

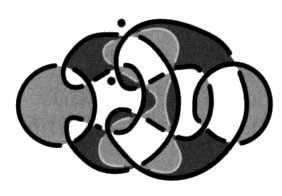 Fig. 4
Fig. 4 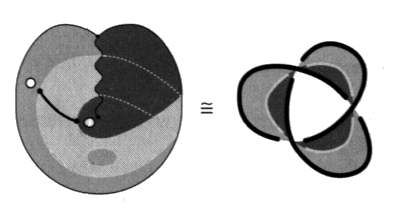 Fig. 6
Fig. 6  Fig. 7
Fig. 7 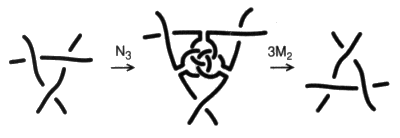 Fig. 8
Fig. 8  Fig. 9
Fig. 9 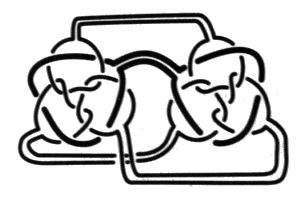 Fig.12
Fig.12 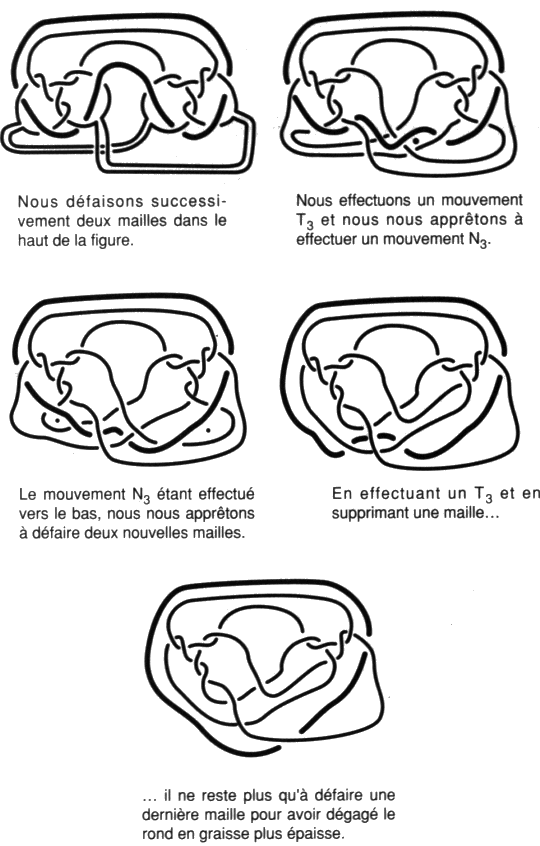 Fig.13
Fig.13
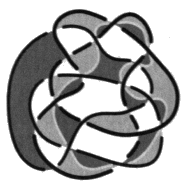 Fig. 14
Fig. 14 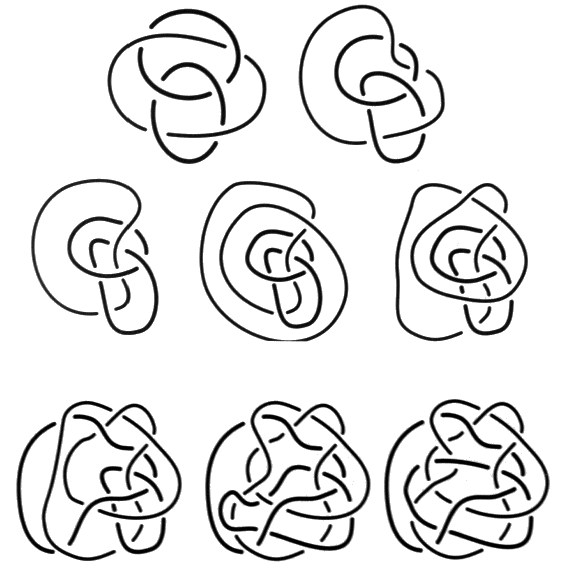 Fig. 17
Fig. 17  Fig. 19
Fig. 19  Fig. 20
Fig. 20 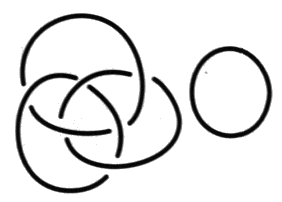 Fig. 21
Fig. 21 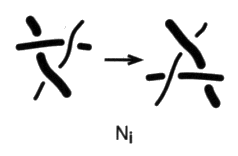 Fig. 22
Fig. 22  Fig. 23
Fig. 23 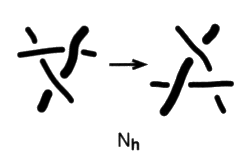 Fig. 24
Fig. 24 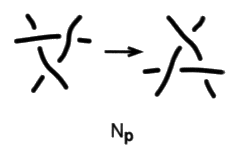 Fig. 26
Fig. 26 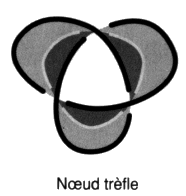 Fig. 27
Fig. 27 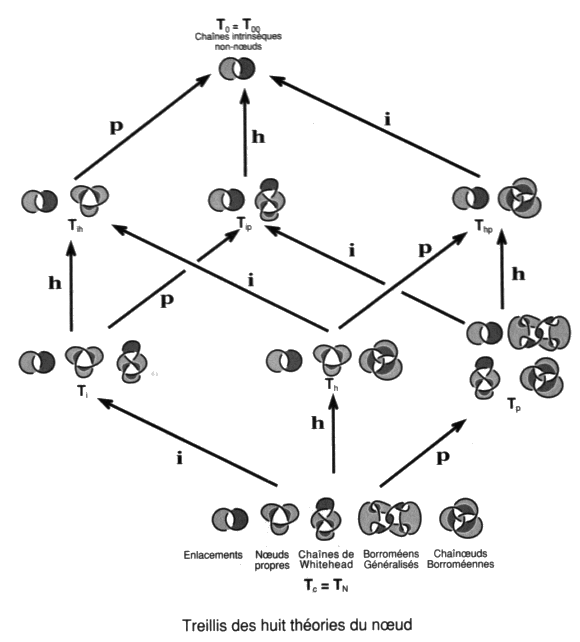
 Fig. 28
Fig. 28 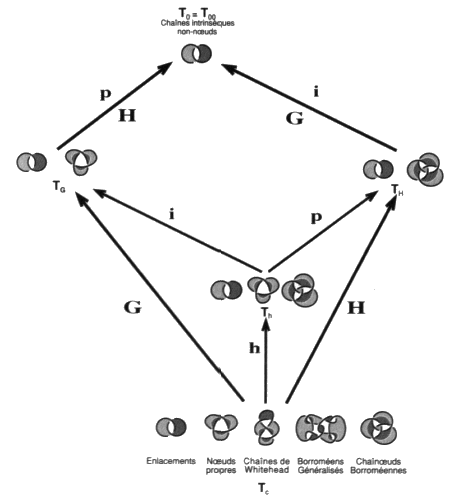
 Fig. 29
Fig. 29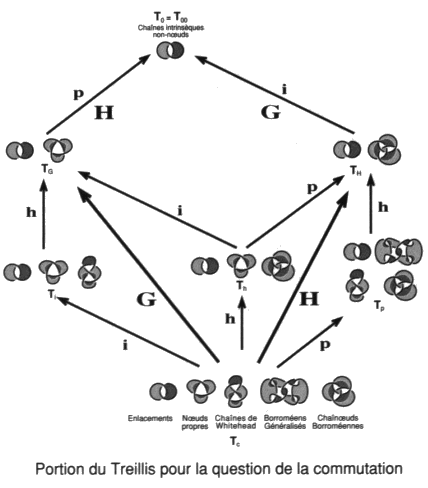
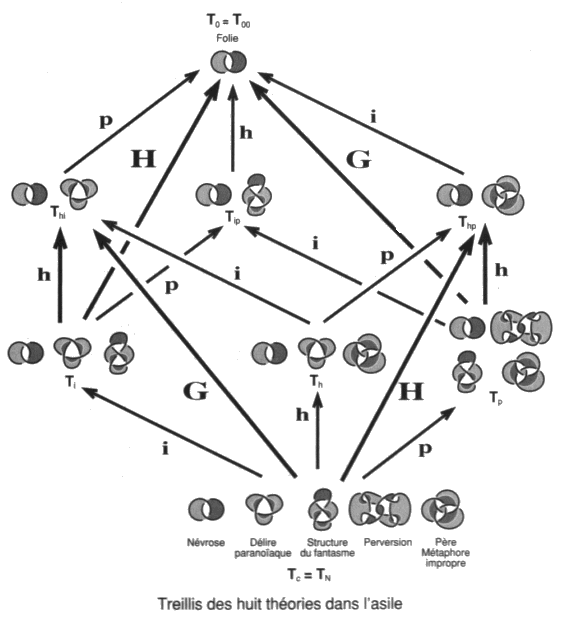
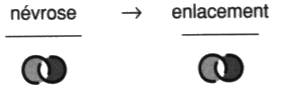
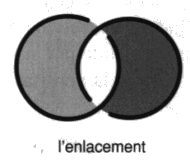 Fig. 30
Fig. 30 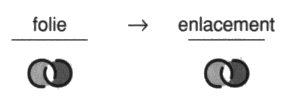
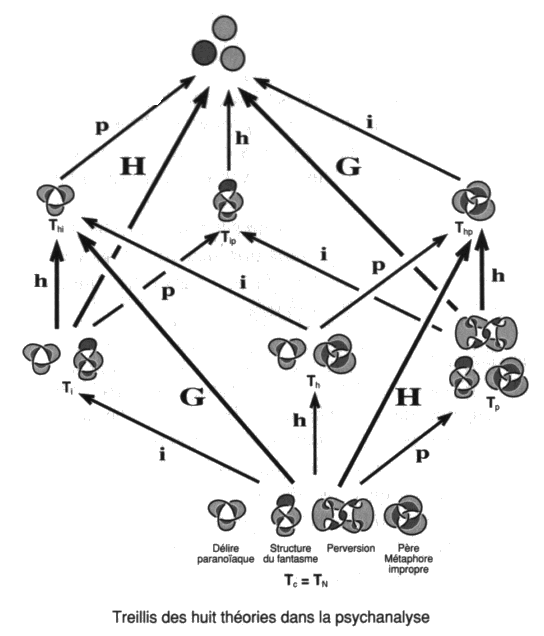
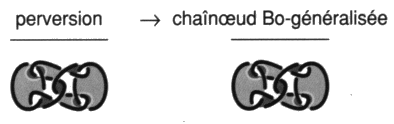
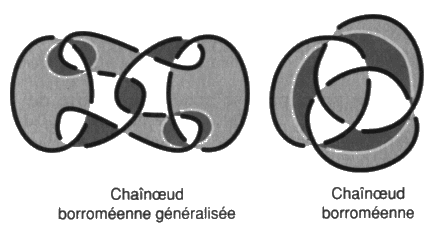 Fig. 31
Fig. 31 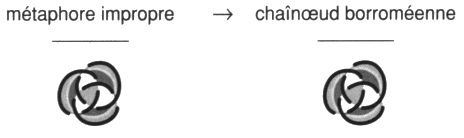

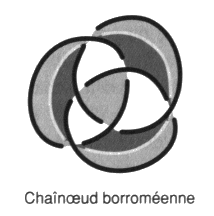 Fig. 32
Fig. 32 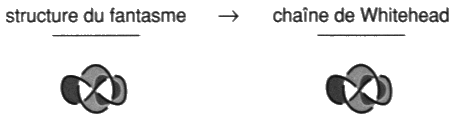
 Fig. 33
Fig. 33 
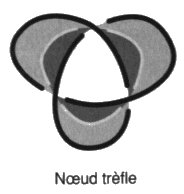 Fig. 34
Fig. 34 
 Fig. 35
Fig. 35 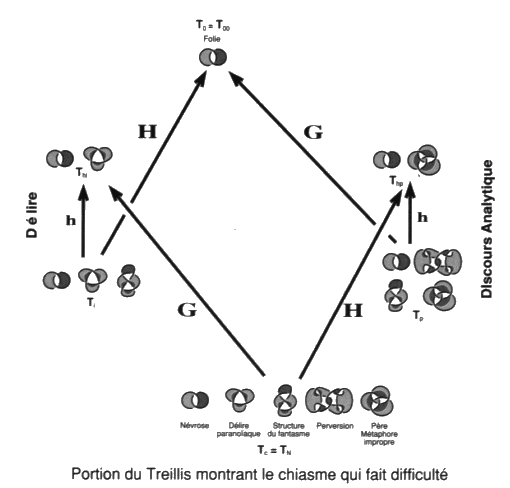
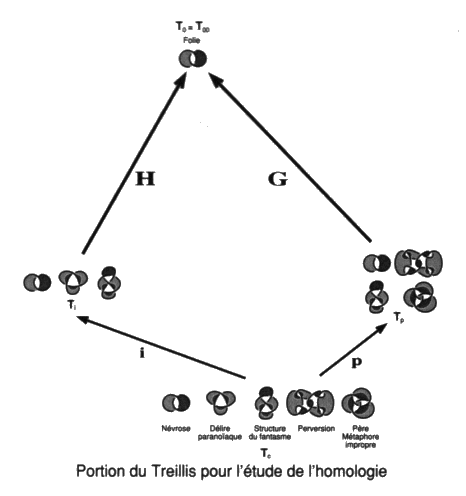
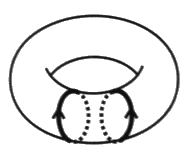 Fig. 36
Fig. 36 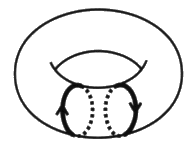 Fig.
37
Fig.
37 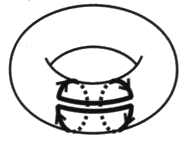 Fig.
38
Fig.
38  Fig. 39
Fig. 39 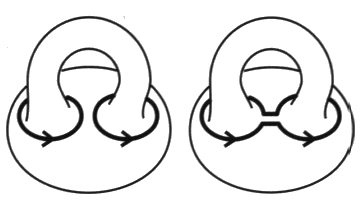 Fig. 40
Fig. 40 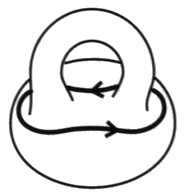 Fig. 41
Fig. 41 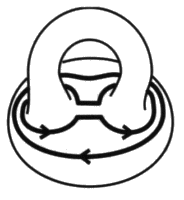 Fig. 42
Fig. 42 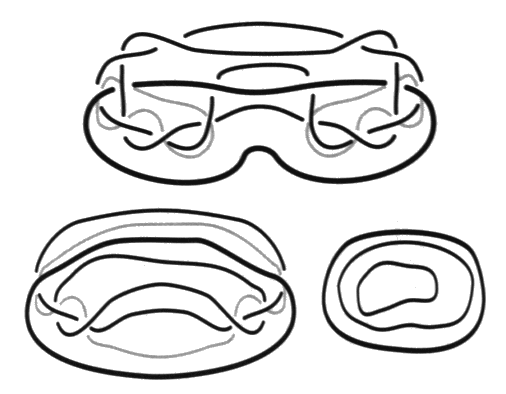 Fig.
46
Fig.
46